ГДЗ по Алгебре 10-11 Класс Номер 123 Алимов — Подробные Ответы

Построить график функции, указать её область определения и множество значений. Выяснить, является ли функция возрастающей (убывающей), является ли функция ограниченной, принимает ли она наибольшее (наименьшее) значение:

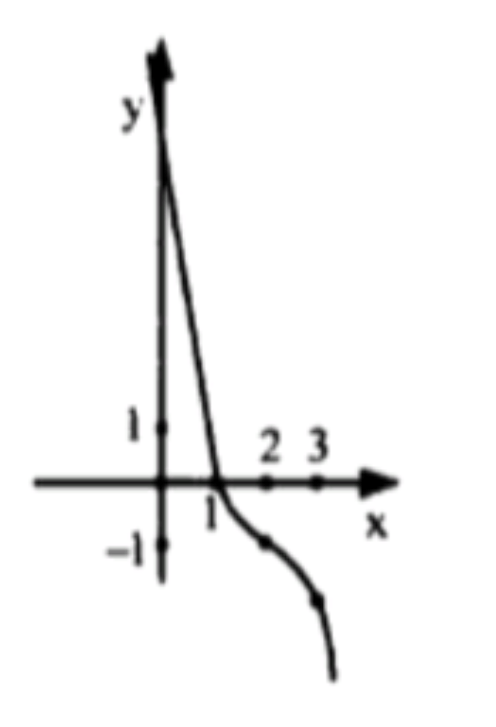
1. у = — (х — 2)3 — 1;
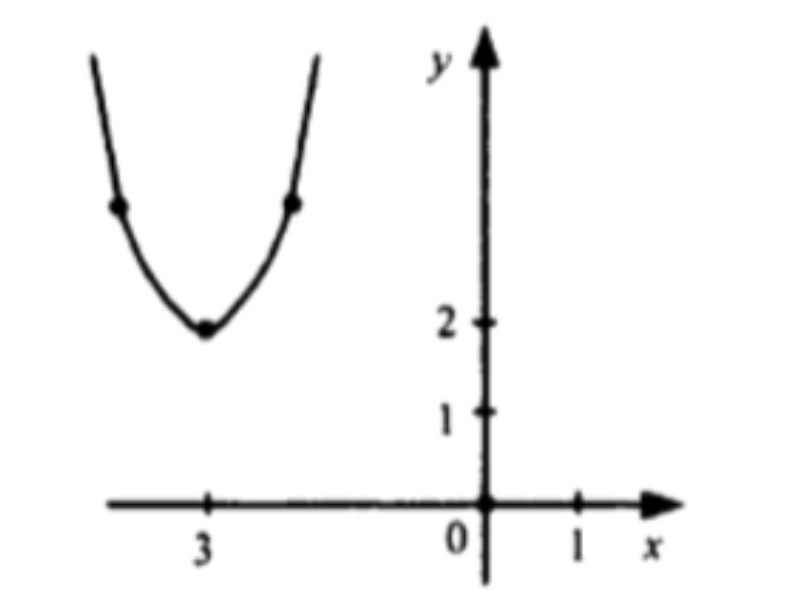
2. у = (х + 3)4 + 2.

1) $y = -(x — 2)^3 — 1$:

Рассмотрим функцию $y=-x^3$:$$$y = -x^3$

Область определения: $x\in \mathbb{R}$

Множество значений: $y\in \mathbb{R}$

• Функция является нечетной;
• Функция убывает на всей числовой прямой;
• Функция не ограничена;

Координаты некоторых точек:
$$\begin{array}{|c|c|c|c|} \hline x & -2 & -1 & 0 \\ \hline y & 8 & 1 & 0 \\ \hline \end{array}$$

Построим график функции $y=-x^3$ и осуществим его сдвиг:

• Вдоль оси абсцисс на 2 единицы вправо;
• Вдоль оси ординат на 1 единицу вниз.

Ответ: убывающая; неограниченная.

2) $y = (x + 3)^4 + 2$:

Рассмотрим функцию $y=x^4$:

Область определения: $x\in \mathbb{R}$

$$Множество значений: $y\ge 0$$$

• Функция является четной;
• Функция убывает на $(-\mathrm{\infty };0)\; и\; возрастает\; на$$(0; +\infty)$
• Функция ограничена снизу;
• Наименьшее значение: $y=0$ при $x=0$$x = 0$

Координаты некоторых точек:
$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 0 & 1 & 16 \\ \hline \end{array}$$

Построим график функции $y=x^4$ и осуществим его сдвиг:

• Вдоль оси абсцисс на 3 единицы влево;
• Вдоль оси ординат на 2 единицы вверх.

Ответ: убывает на $(-\infty; -3)$ и возрастает на $(-3; +\infty)$; ограничена снизу; наименьшее значение $y = 2$ при $x = -3$

1) $y = -(x — 2)^3 — 1$:

Для того, чтобы проанализировать функцию $y = -(x — 2)^3 — 1$, разберём её по частям и рассмотрим её свойства и поведение.

Рассмотрим базовую функцию $y = -x^3$:

Область определения функции: $x\in \mathbb{R}$ , так как кубическая функция определена для всех действительных чисел.

Множество значений функции: $y\in \mathbb{R}$, так как $x^3$ может принимать любые значения, а знак минус лишь меняет знак этих значений.

• Функция $y=-x^3$ является нечетной. Это означает, что для всех значений $x$ справедливо равенство $y(-x)=-y(x)$
• $$Функция $y=-x^3$ убывает на всей числовой прямой. Это можно заметить, так как производная функции $y^{\mathrm{\prime }}=-3x^2$ всегда отрицательна при $x\mathrm{\ne }0$
• Функция $y=-x^3$ неограничена. Для $x\to +\mathrm{\infty }$, $y\to -\mathrm{\infty }$ , и для $x\to -\mathrm{\infty }$, $y\to +\mathrm{\infty }$ . Сдвиг функции $y=-x^3$:
  $y = -x^3$$x \to +\infty$

Вдоль оси абсцисс на 2 единицы вправо: это означает замену x на $x — 2$, то есть функция становится $y = -(x — 2)^3$

Вдоль оси ординат на 1 единицу вниз: это означает, что ко всей функции прибавляется $-1$, и итоговая функция будет $y = -(x — 2)^3 — 1$

Таким образом, данная функция является сдвигом функции $y = -x^3$ вправо на 2 единицы и вниз на 1 единицу.

Анализ функции $y = -(x — 2)^3 — 1$:

• Функция продолжает быть убывающей, так как её базовая форма $y = -x^3$ была убывающей.
• Функция не ограничена сверху и снизу, поскольку кубическая функция $-x^3$ не имеет ограничений по значению $y$$-x^3$

Ответ: Функция $y = -(x — 2)^3 — 1$ является убывающей и неограниченной.

2) $y = (x + 3)^4 + 2$:

Теперь рассмотрим функцию $y = (x + 3)^4 + 2$

Рассмотрим базовую функцию $y = x^4$:

Область определения функции: $x\in \mathbb{R}$, так как функция степени 4 определена для всех действительных чисел.

Множество значений функции: $y\ge 0$ , так как для всех $x$ выражение $x^4$ всегда неотрицательно.

• Функция $y=x^4$ является четной. Это означает, что для всех значений $x$ справедливо равенство $y(-x)=y(x)$
• Функция $y=x^4$убывает на интервале $(-\mathrm{\infty };0)$ и возрастаетна интервале $(0;+\mathrm{\infty }),\; так\; как\; её\; производная$$y’ = 4x^3$ меняет знак в точке $x=0$
• Функция $y=x^4$ ограничена снизу: её наименьшее значение $y=0$ достигается при $x=0$, а для всех других значений $x$ $y\ge 0$. Сдвиг функции $y=x^4$:

Вдоль оси абсцисс на 3 единицы влево: это означает замену $x$ на $x + 3$, и функция становится $y = (x + 3)^4$

Вдоль оси ординат на 2 единицы вверх: это означает, что ко всей функции прибавляется 2, и итоговая функция будет $y=(x+3{)}^4+2$.

Таким образом, данная функция является сдвигом функции $y = x^4$ влево на 3 единицы и вверх на 2 единицы.

Анализ функции $y = (x + 3)^4 + 2$:

Функция будет убывать на интервале $(-\mathrm{\infty };-3)$$(-\infty; -3)и$возрастать на интервале $(-3;+\mathrm{\infty }),\; так\; как\; она\; аналогична\; функции$$(-3; +\infty)$

Функция ограничена снизу: её наименьшее значение достигается в точке $x=-3$ , и равно $y=2$
$x = -3$$y = 2$

Ответ: Функция $y = (x + 3)^4 + 2$ убывает на $(-\infty; -3)$ и возрастает на $(-3; +\infty)$; она ограничена снизу; наименьшее значение $y = 2$ при $x = -3$