ГДЗ по Алгебре 10-11 Класс Номер 1226 Алимов — Подробные Ответы

Массы т пятидесяти детей до года, стоящих на учёте в некоторой районной поликлинике, попадают в промежуток [2; 12]. Распределение значений случайной величины m представлено в частотной таблице:

m [2; 4) [4; 6) [6; 8) [8; 10) [10; 12]

М 2 3 13 26 6

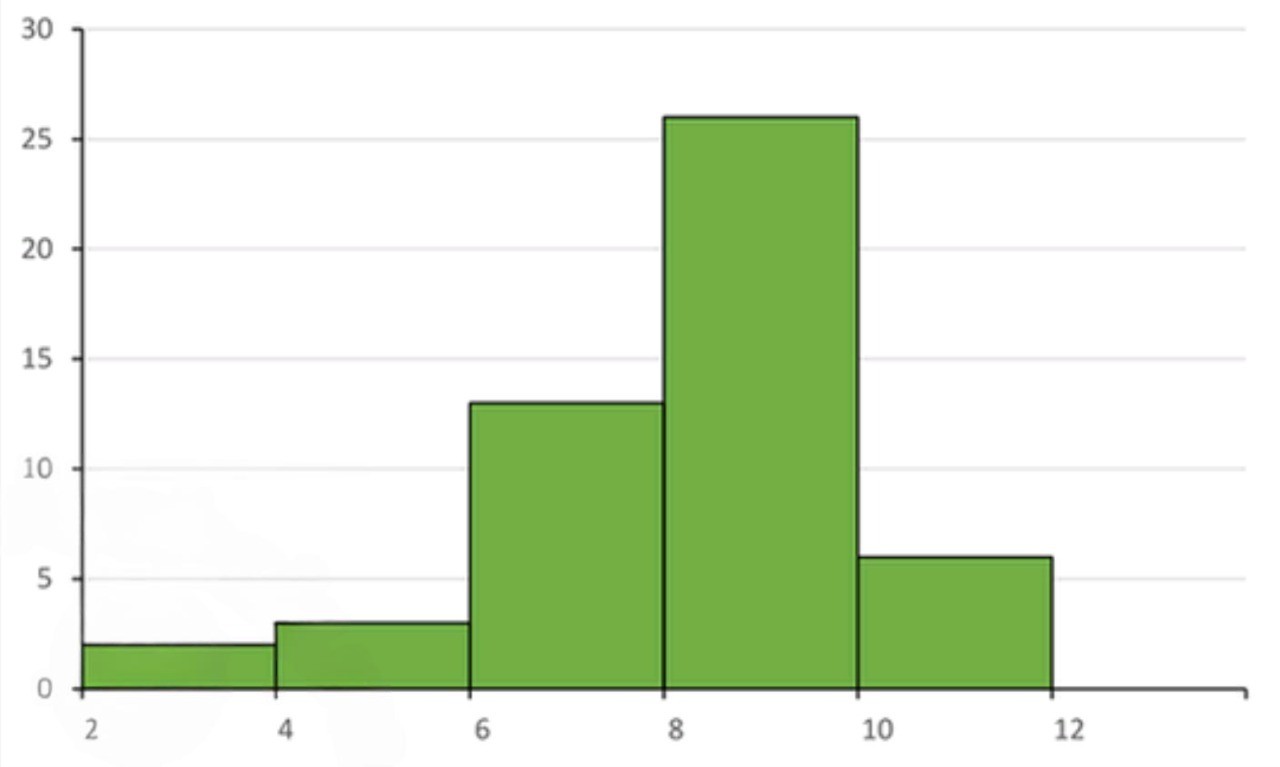
Построить гистограмму распределения значений величины m

1) Таблица распределения по частотам массы $t$ пятидесяти детей до года, стоящих на учете в некоторой районной поликлинике:

2) Гистограмма частот:

Заданные данные:

Здесь $m$ — это интервалы, в которые попадают массы детей, а $M$ — это частоты (или количество детей), чьи массы попадают в эти интервалы. Наши цели могут включать:

1. Нахождение среднего значения массы,
2. Нахождение дисперсии и стандартного отклонения,
3. Построение гистограммы.

Шаг 1: Вычисление среднего значения массы

Среднее значение массы для данной совокупности можно вычислить по формуле для дискретного распределения:

$$\overline{X} = \frac{\sum_{i=1}^{n} x_i \cdot f_i}{\sum_{i=1}^{n} f_i}$$

где:

• $x_i$ — середина интервала $m_i$,
• $f_i$ — частота для каждого интервала.

Чтобы найти середину каждого интервала, мы используем формулу для среднего значения интервала: $x_i = \frac{a_i + b_i}{2}$, где $a_i$ и $b_i$ — границы интервала.

Середины интервалов:

• Для интервала $[2; 4)$: $x_1 = \frac{2 + 4}{2} = 3$
• Для интервала $[4; 6)$: $x_2 = \frac{4 + 6}{2} = 5$
• Для интервала $[6; 8)$: $x_3 = \frac{6 + 8}{2} = 7$
• Для интервала $[8; 10)$: $x_4 = \frac{8 + 10}{2} = 9$
• Для интервала $[10; 12]$: $x_5 = \frac{10 + 12}{2} = 11$

Теперь, вычислим среднее значение массы:

$$\overline{X} = \frac{(3 \cdot 2) + (5 \cdot 3) + (7 \cdot 13) + (9 \cdot 26) + (11 \cdot 6)}{2 + 3 + 13 + 26 + 6}$$

Вычисляем числитель:

$$3 \cdot 2 = 6, \quad 5 \cdot 3 = 15, \quad 7 \cdot 13 = 91, \quad 9 \cdot 26 = 234, \quad 11 \cdot 6 = 66$$

Теперь суммируем:

$$6 + 15 + 91 + 234 + 66 = 412$$

В знаменателе:

$$2 + 3 + 13 + 26 + 6 = 50$$

Итак, среднее значение массы:

$$\overline{X} = \frac{412}{50} = 8,24$$

Ответ: Среднее значение массы $\overline{X} = 8,24$.

Шаг 2: Нахождение дисперсии

Дисперсия для данной совокупности вычисляется по следующей формуле:

$$D = \frac{\sum_{i=1}^{n} (x_i — \overline{X})^2 \cdot f_i}{\sum_{i=1}^{n} f_i}$$

Для этого нам нужно вычислить для каждого интервала $(x_i — \overline{X})^2$, а затем умножить на частоту $f_i$.

Вычислим разницу между серединами интервалов и средним значением:

• Для $x_1 = 3$, $(x_1 — \overline{X})^2 = (3 — 8,24)^2 = (-5,24)^2 = 27,4976$
• Для $x_2 = 5$, $(x_2 — \overline{X})^2 = (5 — 8,24)^2 = (-3,24)^2 = 10,4976$
• Для $x_3 = 7$, $(x_3 — \overline{X})^2 = (7 — 8,24)^2 = (-1,24)^2 = 1,5376$
• Для $x_4 = 9$, $(x_4 — \overline{X})^2 = (9 — 8,24)^2 = (0,76)^2 = 0,5776$
• Для $x_5 = 11$, $(x_5 — \overline{X})^2 = (11 — 8,24)^2 = (2,76)^2 = 7,6176$

Теперь вычислим дисперсию:

$$D = \frac{(27,4976 \cdot 2) + (10,4976 \cdot 3) + (1,5376 \cdot 13) + (0,5776 \cdot 26) + (7,6176 \cdot 6)}{50}$$

Вычислим числитель:

$$27,4976 \cdot 2 = 54,9952, \quad 10,4976 \cdot 3 = 31,4928, \quad 1,5376 \cdot 13 = 19,9888$$ $$0,5776 \cdot 26 = 15,0216, \quad 7,6176 \cdot 6 = 45,7056$$

Суммируем:

$$54,9952 + 31,4928 + 19,9888 + 15,0216 + 45,7056 = 167,204$$

Теперь вычисляем дисперсию:

$$D = \frac{167,204}{50} = 3,34408$$

Ответ: Дисперсия $D = 3,34408$.

Шаг 3: Нахождение стандартного отклонения

Стандартное отклонение — это квадратный корень из дисперсии:

$$\sigma = \sqrt{D} = \sqrt{3,34408} \approx 1,83$$

Ответ: Стандартное отклонение $\sigma \approx 1,83$.

Шаг 4: Построение гистограммы

Гистограмма отображает распределение частот в виде столбцов. Для построения гистограммы, нужно:

1. По оси $x$ отложить интервалы масс (например, [2; 4), [4; 6), и т.д.),
2. По оси $y$ отложить частоты для каждого интервала.

Гистограмма для данных, приведенных в таблице, будет иметь столбцы высотой 2, 3, 13, 26 и 6, что соответствует частотам каждого интервала.