ГДЗ по Алгебре 10-11 Класс Номер 1190 Алимов — Подробные Ответы

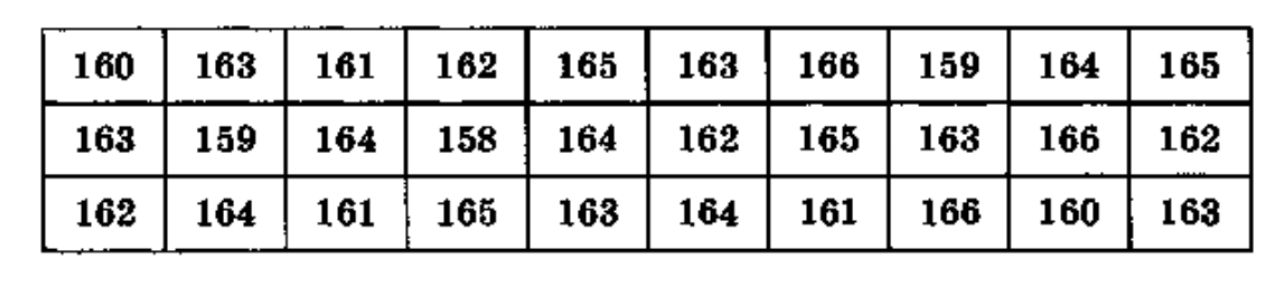
Составить таблицы распределения по частотам (М) и относительным частотам (W), а также полигон частот значений случайной величины Y — ростов 30 девушек спортивной секции гимнастики, приведённых (с точностью до 1 см) в таблице:

1) Таблица распределения роста девушек по частотам и относительным частотам ($N = 30$ — общее число измерений):

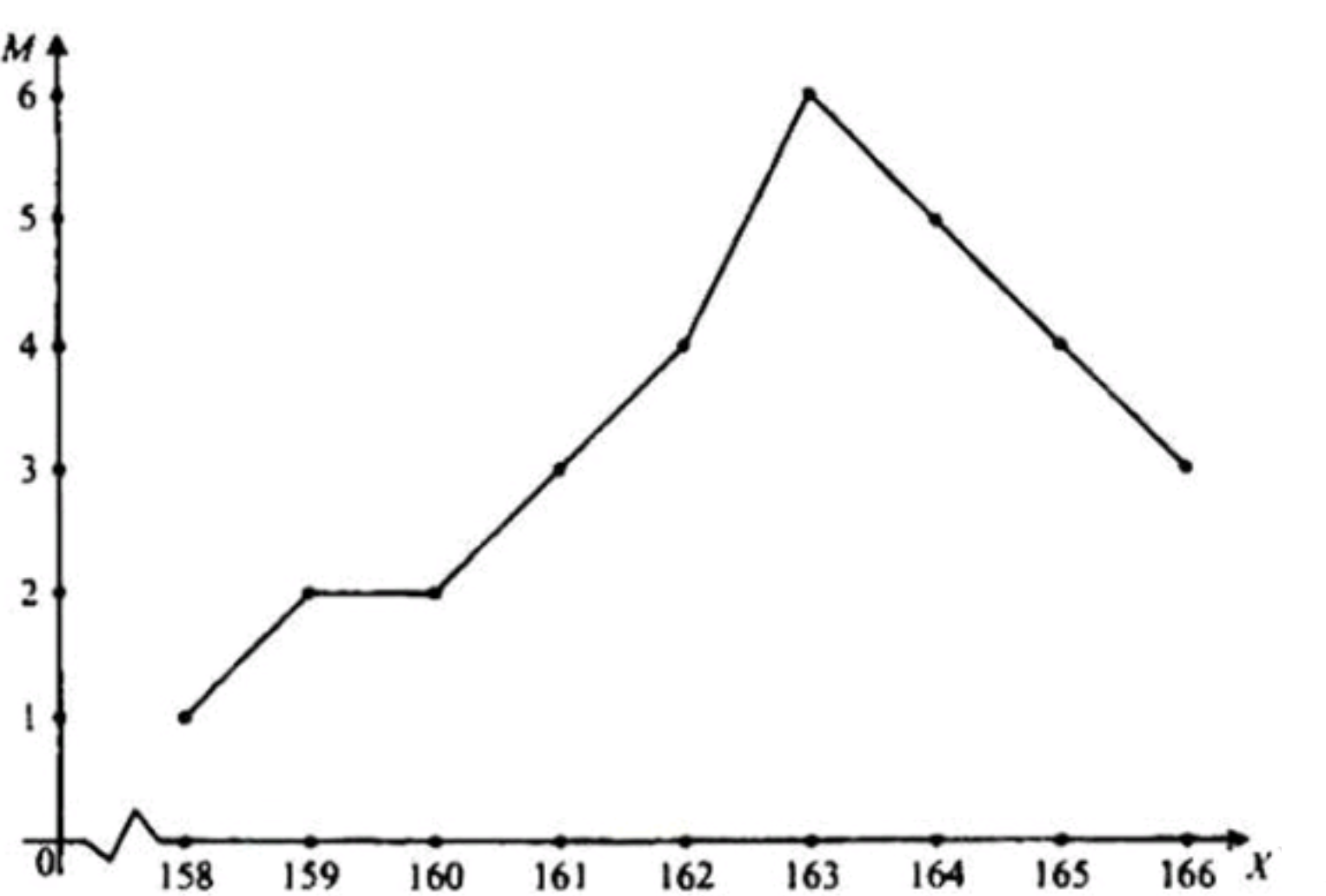
2) Полигон частот:

Данные о ростах 30 девушек, представленные в таблице:

$$\text{Рост (Y)}=160,163,161,162,165,163,159,164,158,163,162,$$

$$\text{Рост (Y)} = 160, 163, 161, 162, 165, 163, 159, 164, 158, 163, 162, 165, 163, 166, 159, 164, 162, 161, 165, 163, 164, 161, 166, 160, 163, 164, 161, 166, 160, 163$$

Количество измерений $N = 30$.

1. Создание таблицы распределения по частотам (M)

Таблица по частотам ($M$) будет отражать количество наблюдений (измерений) для каждого значения роста.

Для этого необходимо посчитать, сколько раз каждое значение роста встречается в выборке. Рассмотрим значения роста и их частоты:

• 158: встречается 1 раз.
• 159: встречается 2 раза.
• 160: встречается 3 раза.
• 161: встречается 4 раза.
• 162: встречается 4 раза.
• 163: встречается 6 раз.
• 164: встречается 5 раз.
• 165: встречается 4 раза.
• 166: встречается 3 раза.

Таким образом, таблица по частотам будет выглядеть следующим образом:

$$\begin{array}{|c|c|} \hline Y (рост) & M (частота) \\ \hline 158 & 1 \\ 159 & 2 \\ 160 & 3 \\ 161 & 4 \\ 162 & 4 \\ 163 & 6 \\ 164 & 5 \\ 165 & 4 \\ 166 & 3 \\ \hline \end{array}$$

2. Таблица распределения по относительным частотам (W)

Относительная частота ($W$) для каждого значения роста вычисляется по формуле:

$$W = \frac{M}{N}$$

где:

• $M$ — частота значения,
• $N$ — общее количество наблюдений.

Для каждого значения роста рассчитываем относительную частоту:

• Для 158: $W = \frac{1}{30}$
• Для 159: $W = \frac{2}{30} = \frac{1}{15}$
• Для 160: $W = \frac{3}{30} = \frac{1}{10}$
• Для 161: $W = \frac{4}{30} = \frac{2}{15}$
• Для 162: $W = \frac{4}{30} = \frac{2}{15}$
• Для 163: $W = \frac{6}{30} = \frac{1}{5}$
• Для 164: $W = \frac{5}{30} = \frac{1}{6}$
• Для 165: $W = \frac{4}{30} = \frac{2}{15}$
• Для 166: $W = \frac{3}{30} = \frac{1}{10}$

Таблица по относительным частотам будет выглядеть так:

$$\begin{array}{|c|c|} \hline Y (рост) & W (относительная частота) \\ \hline 158 & \frac{1}{30} \\ 159 & \frac{2}{30} = \frac{1}{15} \\ 160 & \frac{3}{30} = \frac{1}{10} \\ 161 & \frac{4}{30} = \frac{2}{15} \\ 162 & \frac{4}{30} = \frac{2}{15} \\ 163 & \frac{6}{30} = \frac{1}{5} \\ 164 & \frac{5}{30} = \frac{1}{6} \\ 165 & \frac{4}{30} = \frac{2}{15} \\ 166 & \frac{3}{30} = \frac{1}{10} \\ \hline \end{array}$$

3. Построение полигона частот

Для построения полигона частот, необходимо использовать точки, соответствующие центрам интервалов и частотам. Поскольку рост выражен целыми числами (с точностью до 1 см), центры интервалов — это сами значения роста. Мы будем строить полигон, соединяя точки, где по оси абсцисс отложены значения роста, а по оси ординат — частоты.

Для построения полигона частот:

• Для каждого значения роста $Y$ по оси X ставим точку с абсциссой, равной росту, а по оси Y — частотой $M$.
• Эти точки соединяем линиями.

4. Итоговые таблицы и график

Таблицы распределения по частотам и относительным частотам будут выглядеть следующим образом:

Таблица распределения по частотам $M$:

$$\begin{array}{|c|c|} \hline Y (рост) & M (частота) \\ \hline 158 & 1 \\ 159 & 2 \\ 160 & 3 \\ 161 & 4 \\ 162 & 4 \\ 163 & 6 \\ 164 & 5 \\ 165 & 4 \\ 166 & 3 \\ \hline \end{array}$$

Таблица распределения по относительным частотам $W$:

$$\begin{array}{|c|c|} \hline Y (рост) & W (относительная частота) \\ \hline 158 & \frac{1}{30} \\ 159 & \frac{1}{15} \\ 160 & \frac{1}{10} \\ 161 & \frac{2}{15} \\ 162 & \frac{2}{15} \\ 163 & \frac{1}{5} \\ 164 & \frac{1}{6} \\ 165 & \frac{2}{15} \\ 166 & \frac{1}{10} \\ \hline \end{array}$$