
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 119 Алимов — Подробные Ответы
Изобразить схематически график функции и указать её область определения и множество значений; выяснить, является ли функция ограниченной сверху (снизу):
- у = х6;
- у = х5;
- у = х7;
- у = х^-2;
- у = х^-3;
- у = х6.
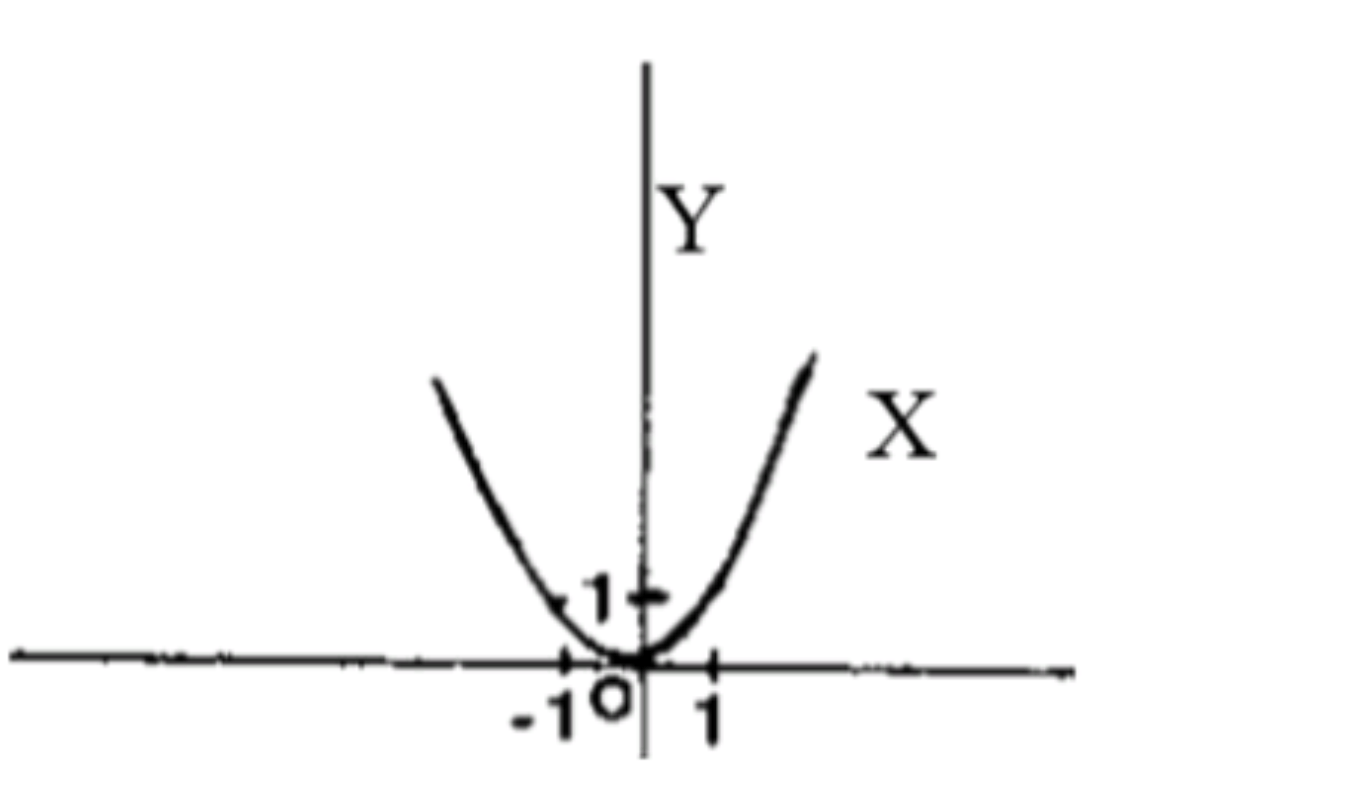
1)
Показатель степени — четное натуральное число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
Ответ: ограничена снизу.
2)
Показатель степени — нечетное натуральное число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
Ответ: не ограничена.
3)
Показатель степени — нечетное натуральное число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
Ответ: не ограничена.
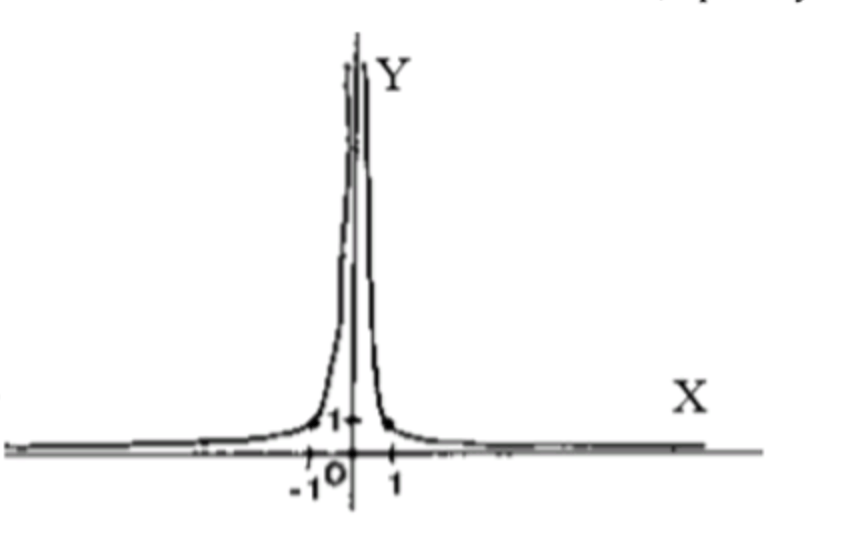
4)
Показатель степени — отрицательное четное целое число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
Ответ: ограничена снизу.
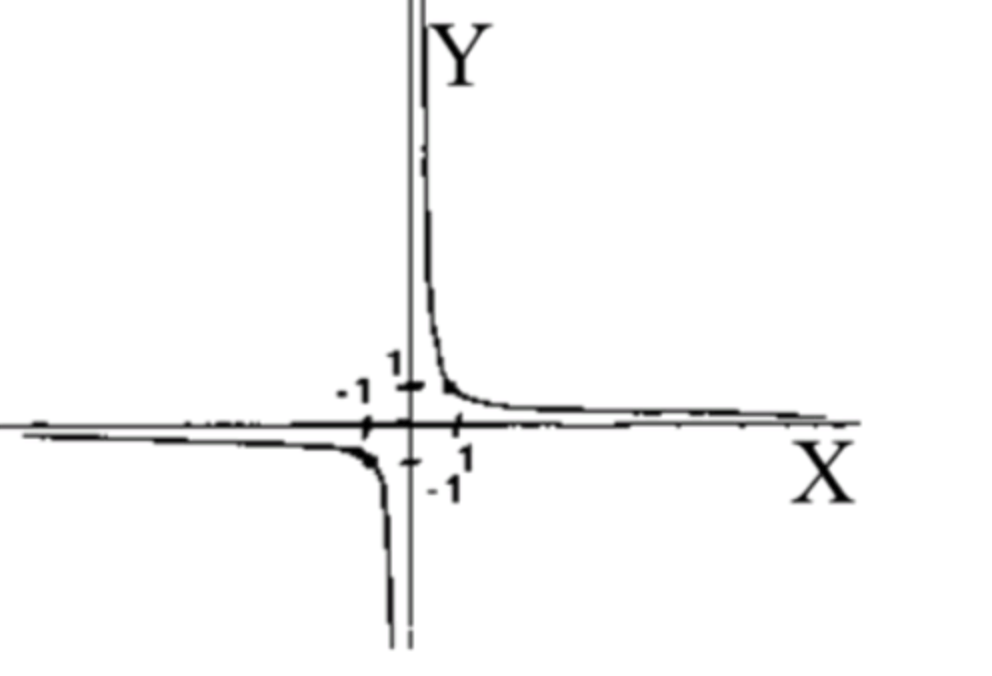
5)
Показатель степени — отрицательное нечетное целое число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
Ответ: не ограничена.
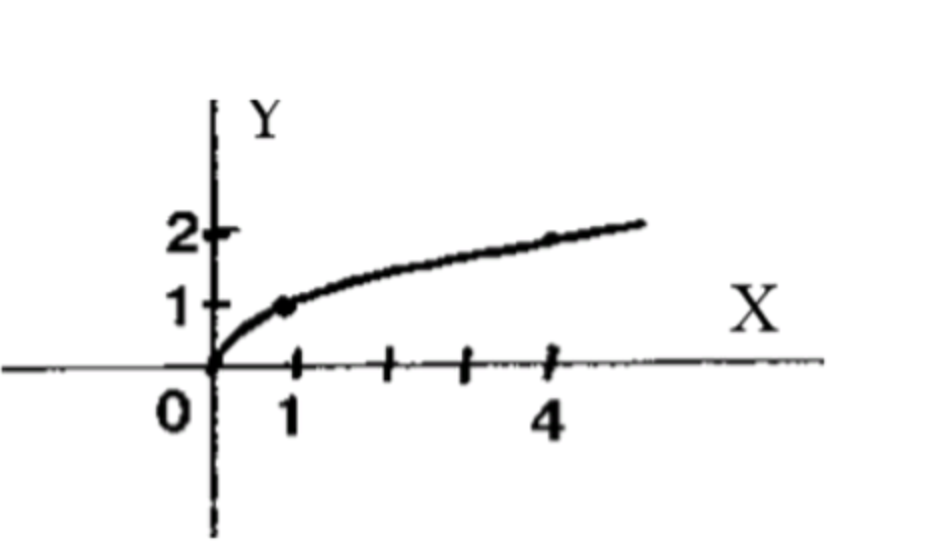
6)
Показатель степени — натуральное число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
Ответ: ограничена снизу.
1)
1. Форма записи и общий анализ
Функция представлена в виде степенной функции:
Здесь основание — переменная , а показатель степени 6 — четное натуральное число.
2. Область определения функции
Функция определена для любых значений , поскольку любое число можно возвести в шестую степень.
3. Множество значений функции
- Возведение в четную степень делает любые числа неотрицательными.
- Минимальное значение: при
- Максимального значения нет, так как при ,
4. Ограниченность функции
Снизу: функция ограничена, так как
Сверху: функция не ограничена, так как
5. Итоговый ответ
2)
1. Анализ функции
Функция степенная:
Здесь показатель степени 5 — нечетное натуральное число.
2. Область определения
Функция определена для всех , так как любое число можно возвести в пятую степень.
3. Множество значений
- Нечетная степень сохраняет знак числа.
- Если , то
- Если , то
- Функция принимает все значения от до
4. Ограниченность функции
- Функция не ограничена ни сверху, ни снизу.
5. Итоговый ответ
3)
1. Анализ функции
Функция степенная:
Здесь показатель степени 7 — нечетное натуральное число.
2. Область определения
Функция определена для всех :
3. Множество значений
- Нечетная степень сохраняет знак числа.
- Если , то
- Если , то
- Функция принимает все значения от до
4. Ограниченность функции
- Функция не ограничена ни сверху, ни снизу.
5. Итоговый ответ
4)
1. Анализ функции
Функция записывается в виде:
Здесь показатель степени -2 — отрицательное четное целое число.
2. Область определения
Функция не определена в точке (деление на ноль запрещено).
3. Множество значений
- Так как всегда положительно, тоже всегда положительно.
- Функция никогда не принимает нулевое или отрицательное значение.
- Максимума нет, но при
4. Ограниченность функции
- Снизу ограничена:
- Сверху не ограничена.
5. Итоговый ответ
5)
1. Анализ функции
Функция записывается в виде:
Здесь показатель степени -3 — отрицательное нечетное целое число.
2. Область определения
Функция не определена в точке
3. Множество значений
- Если , то
- Если , то
- При больших ,
- При ,
4. Ограниченность функции
- Функция не ограничена ни сверху, ни снизу.
5. Итоговый ответ
6)
1. Анализ функции
Функция повторяет случай 1.
2. Область определения
3. Множество значений
4. Ограниченность функции
- Ограничена снизу:
- Не ограничена сверху.
5. Итоговый ответ





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!