ГДЗ по Алгебре 10-11 Класс Номер 1174 Алимов — Подробные Ответы

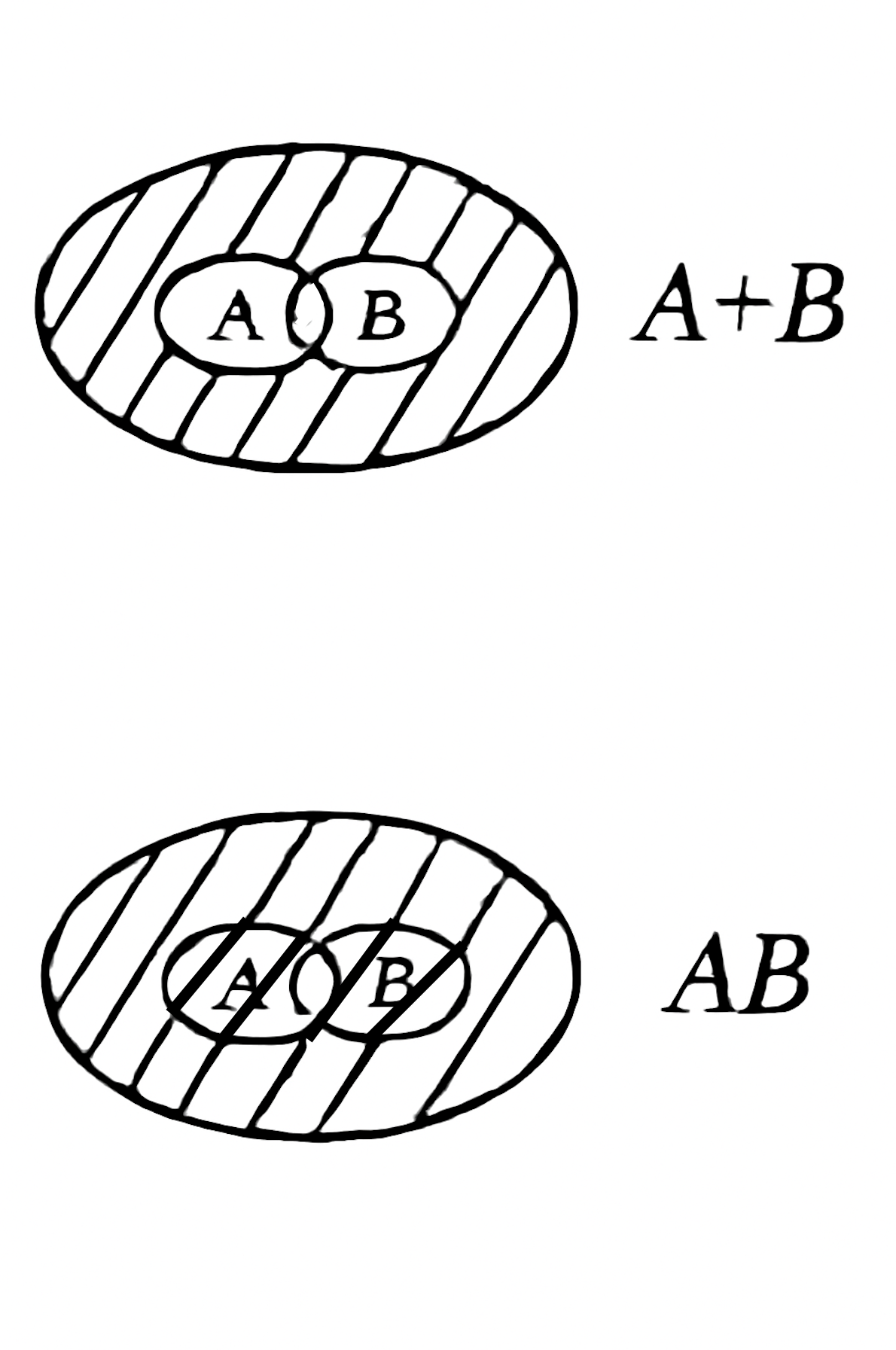
С помощью штриховки (см. рис. 172) проиллюстрировать событие: 1) А + В; 2) АВ, если большой круг на рисунке изображает все элементарные события испытания, с которым связаны события А и В (эти события проиллюстрированы малыми кругами).

1) Проиллюстрируем события с помощью штриховки $A + B$, если большой круг на рисунке изображает все элементарные события испытания, с которыми связаны события $A$ и $B$ (эти события проиллюстрированы малыми кругами).

2) Проиллюстрируем события с помощью штриховки $\overline{A \cap B}$, если большой круг на рисунке изображает все элементарные события испытания, с которыми связаны события $A$ и $B$ (эти события проиллюстрированы малыми кругами).

В данном задании мы будем работать с операциями над множествами, такими как объединение ($A + B$) и дополнение пересечения ($\overline{A \cap B}$), а также иллюстрировать эти операции на диаграммах Веннa.

1. Проиллюстрируем события с помощью штриховки $A + B$, если большой круг на рисунке изображает все элементарные события испытания, с которыми связаны события $A$ и $B$ (эти события проиллюстрированы малыми кругами).

1.1. Теоретическое обоснование

Объединение двух событий $A$ и $B$, которое записывается как $A + B$ (или $A \cup B$ в теории множеств), включает в себя все элементарные события, которые принадлежат хотя бы одному из этих двух событий. Это означает, что элементарное событие будет включаться в объединение, если оно либо принадлежит $A$, либо $B$, либо обоим сразу.

1.2. Штриховка диаграммы Веннa для $A + B$

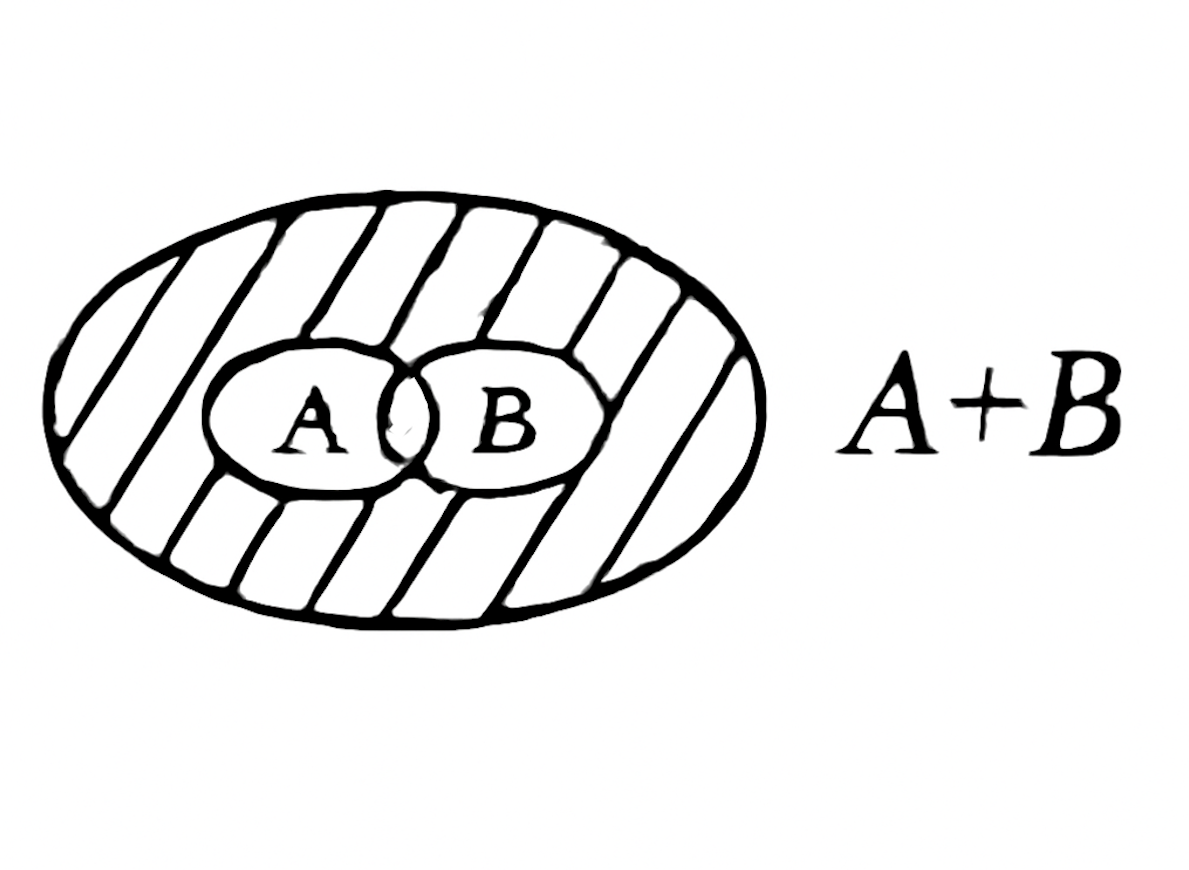
Для визуализации объединения событий $A$ и $B$, на диаграмме Веннa изображены два круга, каждый из которых представляет одно из этих событий (меньшие круги $A$ и $B$) внутри большого круга, который обозначает все элементарные события $\Omega$. Штриховка будет покрывать область, включающую:

• Все элементы в круге $A$ (событие $A$)
• Все элементы в круге $B$ (событие $B$)
• Пересечение двух кругов (общее для обоих событий)

Это связано с тем, что объединение событий включает все элементы, которые могут быть в любом из событий, в том числе в их пересечении.

Иллюстрация:

На диаграмме виден большой круг, внутри которого расположены два маленьких круга, представляющих события $A$ и $B$. Штриховка покрывает все области внутри этих двух кругов, что и означает объединение $A + B$.

2. Проиллюстрируем события с помощью штриховки $\overline{A \cap B}$, если большой круг на рисунке изображает все элементарные события испытания, с которыми связаны события $A$ и $B$ (эти события проиллюстрированы малыми кругами).

2.1. Теоретическое обоснование

Дополнение пересечения двух событий $A$ и $B$, обозначаемое как $\overline{A \cap B}$, включает в себя все элементы из множества $\Omega$ (всех элементарных событий), которые не принадлежат одновременно ни одному из двух событий $A$ и $B$.

Пересечение $A \cap B$ включает в себя все элементы, которые одновременно принадлежат и $A$, и $B$. Дополнение этого пересечения $\overline{A \cap B}$ — это все элементы, которые не находятся в этом пересечении. То есть, штриховка будет включать:

• Все элементы, которые не входят в пересечение $A \cap B$, то есть все элементы, которые либо не принадлежат $A$, либо не принадлежат $B$, либо не принадлежат ни одному из них.

2.2. Штриховка диаграммы Веннa для $\overline{A \cap B}$

Для визуализации дополнения пересечения, на диаграмме Веннa нужно закрасить все области, которые не принадлежат пересечению двух кругов $A$ и $B$. Это включает:

• Внешнюю область, не принадлежащую ни одному из кругов.
• Области, которые находятся только в одном из кругов, но не в пересечении.

Штриховка будет покрывать все области, которые лежат вне пересечения двух кругов.

Иллюстрация:

На диаграмме Веннa видно, как штриховка покрывает все области, которые находятся за пределами пересечения двух кругов $A$ и $B$. Это и есть дополнение пересечения.

Итог

1. $A + B$ — это объединение событий $A$ и $B$. Оно включает в себя все элементы, которые принадлежат хотя бы одному из событий.
2. $\overline{A \cap B}$ — это дополнение пересечения событий $A$ и $B$. Оно включает все элементы, которые не находятся в общих областях этих двух событий.

Общий принцип заключается в том, чтобы правильно изобразить каждое из этих событий на диаграммах Веннa, чтобы четко видеть, какие части пространства событий включаются или исключаются в зависимости от операции над множествами.