ГДЗ по Алгебре 10-11 Класс Учебник 📕 Алимов — Все Части

Алгебра

10-11 класс учебник Алимов

10 класс

Тип

ГДЗ, Решебник.

Автор

Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.

Год

2015-2024.

Издательство

Просвещение.

Описание

Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.

Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.

Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.

Преимущества учебника

Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения.
Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач.
Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам.
Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры.
Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.

Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.

ГДЗ по Алгебре 10-11 Класс Номер 1173 Алимов — Подробные Ответы

Задача

Заполнить последний столбец таблицы, округляя результаты вычислений с точностью до тысячных.

Краткий ответ:

Заполним последний столбец таблицы, округляя результаты вычислений с точностью до тысячных:

№ п/п	Испытание	Число испытаний (N)	Наблюдаемое событие	Частота события (M)	Относительная частота события
1	Брошены два игральных кубика	400	Сумма выпавших чисел равна 2	11	0,028
2	Брошены два игральных кубика	200	Сумма выпавших чисел равна 3	11	0,055
3	Спортсмен стреляет по мишени	300	Попадание по мишени	284	0,946
4	Из колоды карт извлекается одна карта	200	Извлечен туз	23	0,115

Вычисления:

$W_{1} = \frac{M}{N} = \frac{11}{400} = 0, 0275 \approx 0, 028$

$W_1 = \frac{M}{N} = \frac{11}{400} = 0,0275 \approx 0,028$ $W_{2} = \frac{M}{N} = \frac{11}{200} = 0, 055$

$W_2 = \frac{M}{N} = \frac{11}{200} = 0,055$ $W_{3} = \frac{M}{N} = \frac{284}{300} = 0, 94 (6) \approx 0, 946$

$W_3 = \frac{M}{N} = \frac{284}{300} = 0,94(6) \approx 0,946$ $W_4 = \frac{M}{N} = \frac{23}{200} = 0,115$

Подробный ответ:

Нам дана таблица, в которой представлены данные по экспериментам, включая число испытаний, наблюдаемое событие, частоту этого события и его относительную частоту. Необходимо вычислить относительную частоту события, округляя результат до тысячных.

Исходные данные:

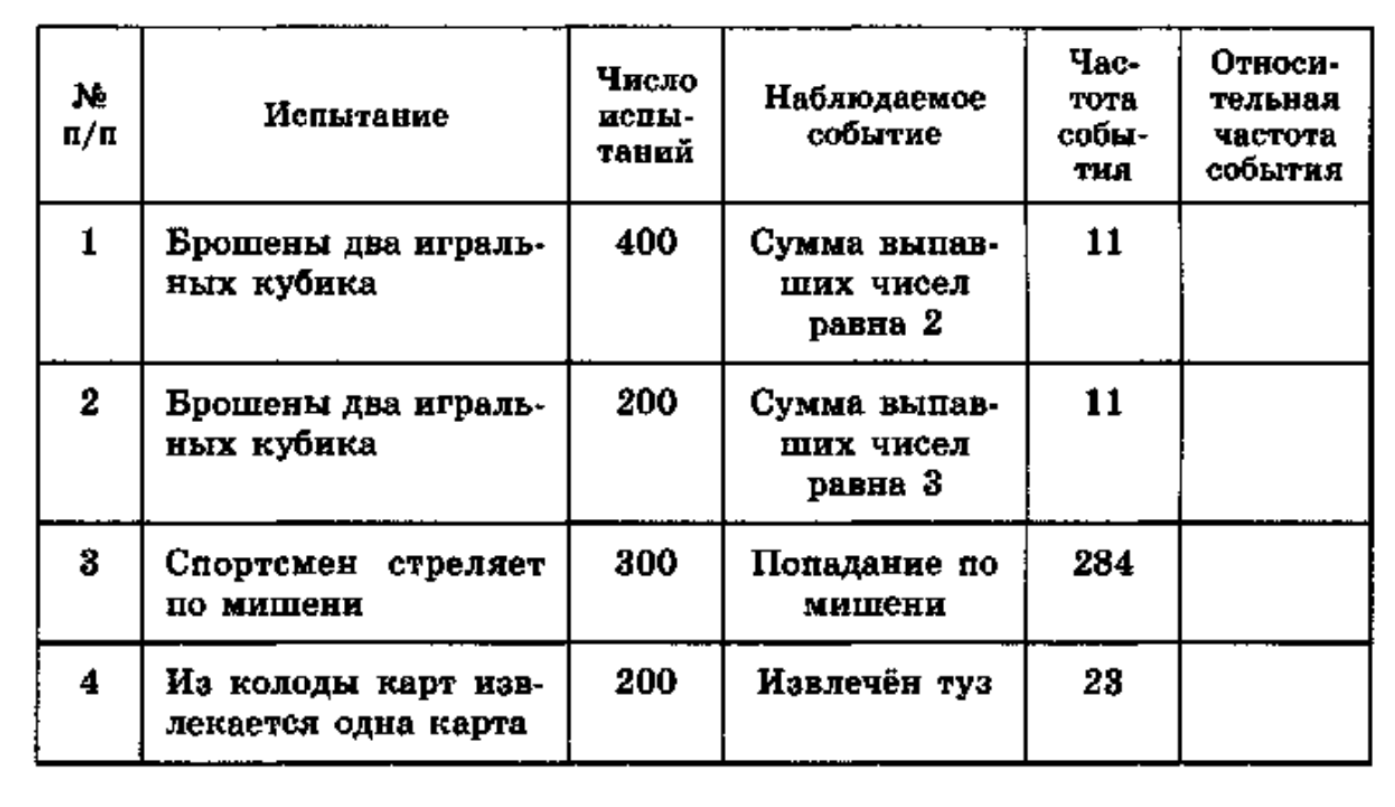
№ п/п	Испытание	Число испытаний (N)	Наблюдаемое событие	Частота события (M)
1	Брошены два игральных кубика	400	Сумма выпавших чисел равна 2	11
2	Брошены два игральных кубика	200	Сумма выпавших чисел равна 3	11
3	Спортсмен стреляет по мишени	300	Попадание по мишени	284
4	Из колоды карт извлекается одна карта	200	Извлечен туз	23

Шаги для вычислений:

Чтобы найти относительную частоту события $W$ , нам нужно использовать формулу:

$W = \frac{M}{N}$

где:

$M$ — частота события (количество успешных исходов),
$N$ — общее количество испытаний (всего попыток).

Относительная частота выражает собой долю успешных исходов от общего числа испытаний и имеет единицу измерения «бездименсионная величина», то есть это просто число между 0 и 1. В данной задаче мы будем округлять результат до тысячных.

1) Брошены два игральных кубика (400 испытаний)

Дано:

$N = 400$ — число испытаний (брошено два игральных кубика 400 раз),
$M = 11$ — частота события (сумма выпавших чисел равна 2, то есть из 400 бросков 11 раз сумма чисел была равна 2).

Используем формулу для расчета относительной частоты:

$W_1 = \frac{M}{N} = \frac{11}{400} = 0,0275.$

Теперь округлим до тысячных:

$W_1 \approx 0,028.$

Ответ для первой строки таблицы: $0,028$ .

2) Брошены два игральных кубика (200 испытаний)

Дано:

$N = 200$ — число испытаний (брошено два игральных кубика 200 раз),
$M = 11$ — частота события (сумма выпавших чисел равна 3, то есть из 200 бросков 11 раз сумма чисел была равна 3).

Используем формулу для расчета относительной частоты:

$W_2 = \frac{M}{N} = \frac{11}{200} = 0,055.$

Ответ для второй строки таблицы: $0,055$ .

3) Спортсмен стреляет по мишени (300 испытаний)

Дано:

$N = 300$ — число испытаний (300 выстрелов),
$M = 284$ — частота события (спортсмен попал в мишень 284 раза).

Используем формулу для расчета относительной частоты:

$W_3 = \frac{M}{N} = \frac{284}{300} = 0,9466667 \ldots$

Теперь округлим до тысячных:

$W_3 \approx 0,946.$

Ответ для третьей строки таблицы: $0,946$ .

4) Из колоды карт извлекается одна карта (200 испытаний)

Дано:

$N = 200$ — число испытаний (извлечено 200 карт),
$M = 23$ — частота события (извлечен туз 23 раза).

Используем формулу для расчета относительной частоты:

$W_4 = \frac{M}{N} = \frac{23}{200} = 0,115.$

Ответ для четвертой строки таблицы: $0,115$ .

Итоговые результаты:

Мы рассчитали относительные частоты для каждого события и заполнили последний столбец таблицы:

№ п/п	Испытание	Число испытаний (N)	Наблюдаемое событие	Частота события (M)	Относительная частота события
1	Брошены два игральных кубика	400	Сумма выпавших чисел равна 2	11	0,028
2	Брошены два игральных кубика	200	Сумма выпавших чисел равна 3	11	0,055
3	Спортсмен стреляет по мишени	300	Попадание по мишени	284	0,946
4	Из колоды карт извлекается одна карта	200	Извлечен туз	23	0,115

Выводы:

Для всех наблюдаемых событий относительная частота была вычислена по формуле $W = \frac{M}{N}$ , где $M$ — частота события, а $N$ — число испытаний.
Результаты были округлены до тысячных, как указано в задаче.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Задачи для внеклассной работы