Краткий ответ:
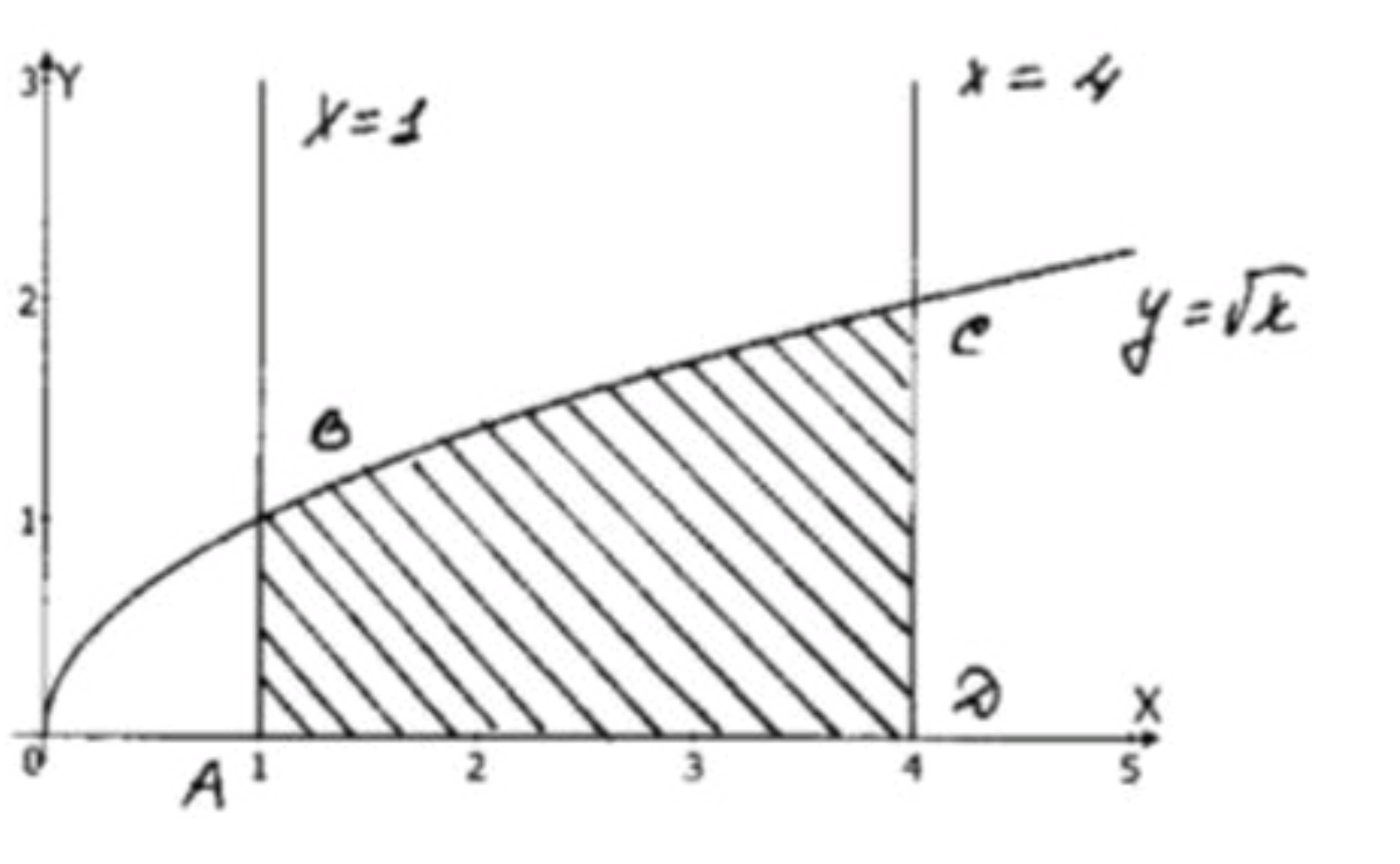
1) y = x y = \sqrt{x} x = 1 x = 1 x = 4 x = 4 y = 0 y = 0
Пересечения с осью x x
x > 0 , отсюда x ≠ 0 ; \sqrt{x} > 0, \text{ отсюда } x \neq 0;
Площадь криволинейной трапеции:
S = ∫ 1 4 x d x = ∫ 1 4 x 1 2 d x = ( x 3 2 3 2 ) ∣ 1 4 = ( 2 3 x x ) ∣ 1 4 ; S = \int_{1}^{4} \sqrt{x} \, dx = \int_{1}^{4} x^{\frac{1}{2}} \, dx = \left( \frac{x^{\frac{3}{2}}}{\frac{3}{2}} \right) \bigg|_{1}^{4} = \left( \frac{2}{3} x \sqrt{x} \right) \bigg|_{1}^{4}; S = 2 3 ⋅ 4 4 − 2 3 ⋅ 1 1 = 8 3 ⋅ 2 − 2 3 = 16 3 − 2 3 = 14 3 = 4 2 3 . S = \frac{2}{3} \cdot 4 \sqrt{4} — \frac{2}{3} \cdot 1 \sqrt{1} = \frac{8}{3} \cdot 2 — \frac{2}{3} = \frac{16}{3} — \frac{2}{3} = \frac{14}{3} = 4 \frac{2}{3}.
Ответ: 4 2 3 4 \frac{2}{3}
2) y = cos x y = \cos x x = 0 x = 0 x = π 3 x = \frac{\pi}{3} y = 0 y = 0
Пересечения с осью x x
cos x ⩾ 0 ; \cos x \geqslant 0; − arccos 0 + 2 π n < x < arccos 0 + 2 π n ; -\arccos 0 + 2\pi n < x < \arccos 0 + 2\pi n; − π 2 + 2 π n < x < π 2 + 2 π n ; -\frac{\pi}{2} + 2\pi n < x < \frac{\pi}{2} + 2\pi n; 0 < x < π 3 ; 0 < x < \frac{\pi}{3};
Площадь криволинейной трапеции:
S = ∫ 0 π 3 cos x d x = sin x ∣ 0 π 3 = sin π 3 − sin 0 = 3 2 ; S = \int_{0}^{\frac{\pi}{3}} \cos x \, dx = \sin x \bigg|_{0}^{\frac{\pi}{3}} = \sin \frac{\pi}{3} — \sin 0 = \frac{\sqrt{3}}{2};
Ответ: 3 2 \frac{\sqrt{3}}{2}
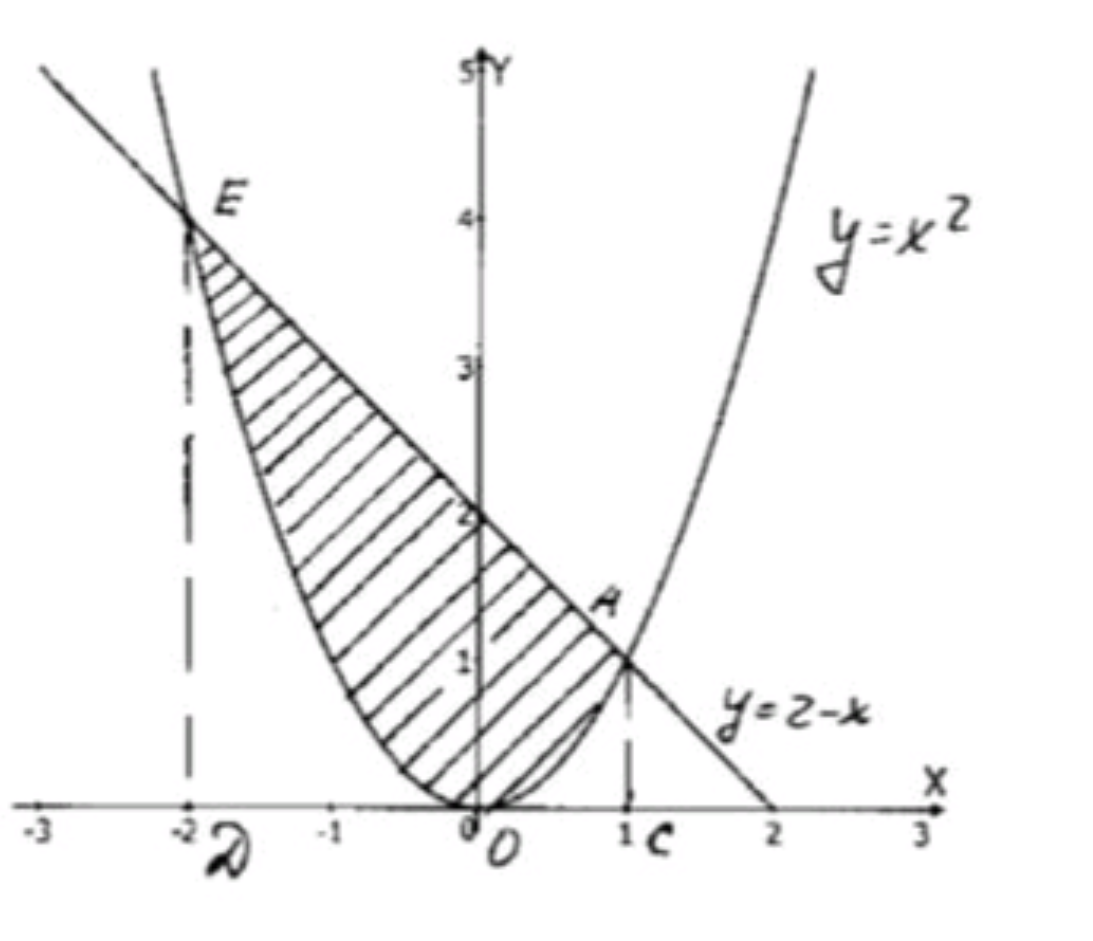
3) y = x 2 y = x^2 y = 2 − x y = 2 — x
Точки пересечения функций:
x 2 = 2 − x ; x^2 = 2 — x; x 2 + x − 2 = 0 ; x^2 + x — 2 = 0; D = 1 2 + 4 ⋅ 2 = 1 + 8 = 9 , тогда: D = 1^2 + 4 \cdot 2 = 1 + 8 = 9, \text{ тогда: } x 1 = − 1 − 3 2 = − 2 и x 2 = − 1 + 3 2 = 1 ; x_1 = \frac{-1 — 3}{2} = -2 \quad \text{и} \quad x_2 = \frac{-1 + 3}{2} = 1;
Площадь криволинейной трапеции:
S = ∫ − 2 1 ( 2 − x − x 2 ) d x = ( 2 x − x 2 2 − x 3 3 ) ∣ − 2 1 = S = \int_{-2}^{1} (2 — x — x^2) \, dx = \left( 2x — \frac{x^2}{2} — \frac{x^3}{3} \right) \bigg|_{-2}^{1} = = 2 ⋅ 1 − 1 2 2 − 1 3 3 − ( 2 ⋅ ( − 2 ) + ( − 2 ) 2 2 + ( − 2 ) 3 3 ) = = 2 \cdot 1 — \frac{1^2}{2} — \frac{1^3}{3} — \left( 2 \cdot (-2) + \frac{(-2)^2}{2} + \frac{(-2)^3}{3} \right) = = 2 − 1 2 − 1 3 + 4 + 4 2 − 8 3 = = 2 — \frac{1}{2} — \frac{1}{3} + 4 + \frac{4}{2} — \frac{8}{3} = = 6 + 3 2 − 9 3 = 6 + 1.5 − 3 = 4.5 ; = 6 + \frac{3}{2} — \frac{9}{3} = 6 + 1.5 — 3 = 4.5;
Ответ: 4.5 4.5
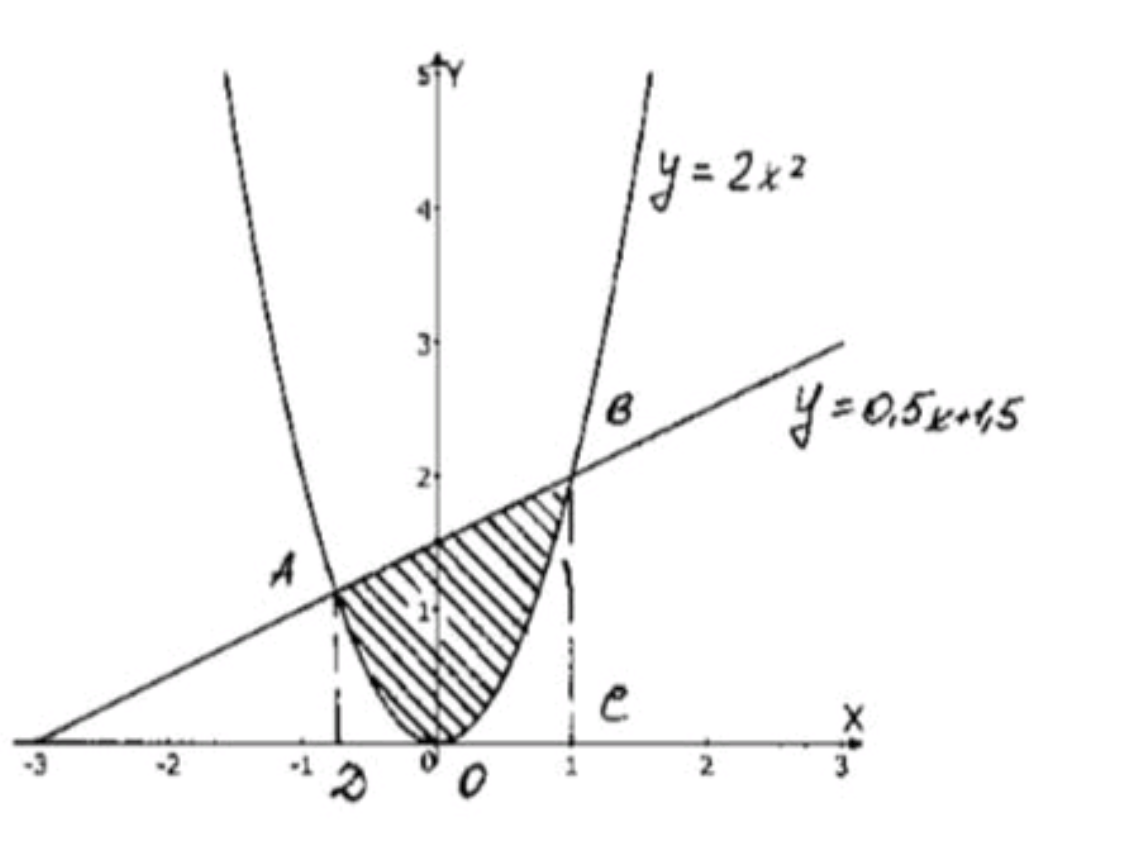
4) y = 2 x 2 y = 2x^2 y = 0.5 x + 1.5 y = 0.5x + 1.5
Точки пересечения функций:
2 x 2 = 0.5 x + 1.5 ; 2x^2 = 0.5x + 1.5; 2 x 2 − 0.5 x − 1.5 = 0 ; 2x^2 — 0.5x — 1.5 = 0; 4 x 2 − x − 3 = 0 ; 4x^2 — x — 3 = 0; D = 1 2 + 4 ⋅ 4 ⋅ 3 = 1 + 48 = 49 , тогда: D = 1^2 + 4 \cdot 4 \cdot 3 = 1 + 48 = 49, \text{ тогда: } x 1 = 1 − 7 2 ⋅ 4 = − 6 8 = − 3 4 и x 2 = 1 + 7 2 ⋅ 4 = 1 ; x_1 = \frac{1 — 7}{2 \cdot 4} = \frac{-6}{8} = -\frac{3}{4} \quad \text{и} \quad x_2 = \frac{1 + 7}{2 \cdot 4} = 1;
Площадь криволинейной трапеции:
S = ∫ − 3 4 1 ( 0.5 x + 1.5 − 2 x 2 ) d x = ( 0.5 ⋅ x 2 2 + 1.5 x − 2 ⋅ x 3 3 ) ∣ − 3 4 1 = S = \int_{-\frac{3}{4}}^{1} (0.5x + 1.5 — 2x^2) \, dx = \left( 0.5 \cdot \frac{x^2}{2} + 1.5x — 2 \cdot \frac{x^3}{3} \right) \bigg|_{-\frac{3}{4}}^{1} = = 0.5 ⋅ 1 2 2 + 1.5 ⋅ 1 − 2 ⋅ 1 3 3 − ( 0.5 ⋅ ( − 3 4 ) 2 2 + 1.5 ⋅ ( − 3 4 ) − 2 ⋅ ( − 3 4 ) 3 3 ) = = 0.5 \cdot \frac{1^2}{2} + 1.5 \cdot 1 — 2 \cdot \frac{1^3}{3} — \left( 0.5 \cdot \frac{\left( -\frac{3}{4} \right)^2}{2} + 1.5 \cdot \left( -\frac{3}{4} \right) — 2 \cdot \frac{\left( -\frac{3}{4} \right)^3}{3} \right) = = 1 4 + 3 2 − 2 3 − ( 9 64 ⋅ 0.5 − 9 8 + 27 96 ) = = \frac{1}{4} + \frac{3}{2} — \frac{2}{3} — \left( \frac{9}{64} \cdot 0.5 — \frac{9}{8} + \frac{27}{96} \right) = = 1 4 + 3 2 − 2 3 − ( 9 128 − 9 8 + 27 96 ) = = \frac{1}{4} + \frac{3}{2} — \frac{2}{3} — \left( \frac{9}{128} — \frac{9}{8} + \frac{27}{96} \right) = = 1 4 + 3 2 − 2 3 − ( 9 128 − 144 128 + 36 128 ) = = \frac{1}{4} + \frac{3}{2} — \frac{2}{3} — \left( \frac{9}{128} — \frac{144}{128} + \frac{36}{128} \right) = = 1 4 + 3 2 − 2 3 − ( − 99 128 ) = = \frac{1}{4} + \frac{3}{2} — \frac{2}{3} — \left( \frac{-99}{128} \right) = = 1 4 + 3 2 − 2 3 + 99 128 = = \frac{1}{4} + \frac{3}{2} — \frac{2}{3} + \frac{99}{128} = = 32 128 + 192 128 − 85.33 128 + 99 128 = = \frac{32}{128} + \frac{192}{128} — \frac{85.33}{128} + \frac{99}{128} = = 32 + 192 − 85.33 + 99 128 = 237.67 128 = 1 151 192 . = \frac{32 + 192 — 85.33 + 99}{128} = \frac{237.67}{128} = 1 \frac{151}{192}.
Ответ: 1 151 192 1 \frac{151}{192}
Подробный ответ:
1) Найти площадь, ограниченную графиком y = x y = \sqrt{x} x = 1 x = 1 x = 4 x = 4 y = 0 y = 0
Шаг 1: Уточнение границ и условий
График функции:
y = x = x 1 / 2 y = \sqrt{x} = x^{1/2}
Ограничивающие линии:
Вертикальные: x = 1 x = 1 x = 4 x = 4 Горизонтальная: y = 0 y = 0 O X OX Шаг 2: Формула для площади
Площадь под графиком между x = 1 x = 1 x = 4 x = 4
S = ∫ 1 4 x d x = ∫ 1 4 x 1 / 2 d x S = \int_{1}^{4} \sqrt{x} \, dx = \int_{1}^{4} x^{1/2} \, dx
Шаг 3: Вычисление интеграла
Применяем формулу:
∫ x n d x = x n + 1 n + 1 + C \int x^{n} \, dx = \frac{x^{n+1}}{n+1} + C
В нашем случае n = 1 2 n = \frac{1}{2}
∫ x 1 / 2 d x = x 3 / 2 3 / 2 = 2 3 x 3 / 2 = 2 3 x x \int x^{1/2} \, dx = \frac{x^{3/2}}{3/2} = \frac{2}{3} x^{3/2} = \frac{2}{3} x \sqrt{x}
Шаг 4: Подстановка пределов интегрирования
S = 2 3 x x ∣ 1 4 = 2 3 ⋅ 4 ⋅ 4 − 2 3 ⋅ 1 ⋅ 1 S = \left. \frac{2}{3} x \sqrt{x} \right|_{1}^{4} = \frac{2}{3} \cdot 4 \cdot \sqrt{4} — \frac{2}{3} \cdot 1 \cdot \sqrt{1} = 2 3 ⋅ 4 ⋅ 2 − 2 3 = 16 3 − 2 3 = 14 3 = \frac{2}{3} \cdot 4 \cdot 2 — \frac{2}{3} = \frac{16}{3} — \frac{2}{3} = \frac{14}{3}
Ответ:
S = 14 3 = 4 2 3 S = \frac{14}{3} = 4 \frac{2}{3}
2) Найти площадь под графиком y = cos x y = \cos x x = 0 x = 0 x = π 3 x = \frac{\pi}{3}
Шаг 1: Уточнение границ
Функция: y = cos x y = \cos x
Ограничения: x = 0 x = 0 x = π 3 x = \frac{\pi}{3} y = 0 y = 0 cos x ≥ 0 \cos x \geq 0 x x
Шаг 2: Интеграл
S = ∫ 0 π 3 cos x d x S = \int_{0}^{\frac{\pi}{3}} \cos x \, dx
Шаг 3: Найдём первообразную
∫ cos x d x = sin x \int \cos x \, dx = \sin x
Шаг 4: Подстановка пределов
S = sin ( π 3 ) − sin ( 0 ) = 3 2 − 0 = 3 2 S = \sin \left( \frac{\pi}{3} \right) — \sin(0) = \frac{\sqrt{3}}{2} — 0 = \frac{\sqrt{3}}{2}
Ответ:
S = 3 2 S = \frac{\sqrt{3}}{2}
3) Найти площадь между кривыми y = x 2 y = x^2 y = 2 − x y = 2 — x
Шаг 1: Найдём точки пересечения
Решим уравнение:
x 2 = 2 − x ⇒ x 2 + x − 2 = 0 x^2 = 2 — x \Rightarrow x^2 + x — 2 = 0
Найдём дискриминант:
D = 1 2 − 4 ⋅ 1 ⋅ ( − 2 ) = 1 + 8 = 9 D = 1^2 — 4 \cdot 1 \cdot (-2) = 1 + 8 = 9
Корни:
x 1 = − 1 − 3 2 = − 2 , x 2 = − 1 + 3 2 = 1 x_1 = \frac{-1 — 3}{2} = -2, \quad x_2 = \frac{-1 + 3}{2} = 1
Шаг 2: Определим, какая функция выше
Проверим, например, в точке x = 0 x = 0
y = x 2 = 0 y = x^2 = 0 y = 2 − x = 2 y = 2 — x = 2 Значит, на этом отрезке y = 2 − x y = 2 — x y = x 2 y = x^2
Шаг 3: Формула площади между двумя кривыми
S = ∫ − 2 1 [ ( 2 − x ) − x 2 ] d x = ∫ − 2 1 ( 2 − x − x 2 ) d x S = \int_{-2}^{1} \left[ (2 — x) — x^2 \right] \, dx = \int_{-2}^{1} (2 — x — x^2) \, dx
Шаг 4: Интегрируем
∫ ( 2 − x − x 2 ) d x = 2 x − x 2 2 − x 3 3 \int (2 — x — x^2) \, dx = 2x — \frac{x^2}{2} — \frac{x^3}{3}
Шаг 5: Подстановка пределов
В точке x = 1 x = 1
2 ⋅ 1 − 1 2 2 − 1 3 3 = 2 − 1 2 − 1 3 2 \cdot 1 — \frac{1^2}{2} — \frac{1^3}{3} = 2 — \frac{1}{2} — \frac{1}{3}
В точке x = − 2 x = -2
2 ⋅ ( − 2 ) − ( − 2 ) 2 2 − ( − 2 ) 3 3 = − 4 − 2 + 8 3 = − 6 + 8 3 2 \cdot (-2) — \frac{(-2)^2}{2} — \frac{(-2)^3}{3} = -4 — 2 + \frac{8}{3} = -6 + \frac{8}{3}
Итак, площадь:
S = [ 2 − 1 2 − 1 3 ] − [ − 6 + 8 3 ] = ( 12 − 3 − 2 6 ) + ( 6 − 8 3 ) = 7 6 + ( 18 − 8 3 ) = 7 6 + 10 3 = 7 6 + 20 6 = 27 6 = 4.5 S = \left[ 2 — \frac{1}{2} — \frac{1}{3} \right] — \left[ -6 + \frac{8}{3} \right] = \left( \frac{12 — 3 — 2}{6} \right) + \left( 6 — \frac{8}{3} \right) = \frac{7}{6} + \left( \frac{18 — 8}{3} \right) = \frac{7}{6} + \frac{10}{3} = \frac{7}{6} + \frac{20}{6} = \frac{27}{6} = 4.5
Ответ:
S = 4.5 S = 4.5
4) Найти площадь между кривыми y = 2 x 2 y = 2x^2 y = 0.5 x + 1.5 y = 0.5x + 1.5
Шаг 1: Найдём точки пересечения
2 x 2 = 0.5 x + 1.5 ⇒ 2 x 2 − 0.5 x − 1.5 = 0 ⇒ 4 x 2 − x − 3 = 0 2x^2 = 0.5x + 1.5 \Rightarrow 2x^2 — 0.5x — 1.5 = 0 \Rightarrow 4x^2 — x — 3 = 0
Шаг 2: Найдём корни
Дискриминант:
D = ( − 1 ) 2 − 4 ⋅ 4 ⋅ ( − 3 ) = 1 + 48 = 49 D = (-1)^2 — 4 \cdot 4 \cdot (-3) = 1 + 48 = 49
Корни:
x 1 = 1 − 7 8 = − 6 8 = − 3 4 , x 2 = 1 + 7 8 = 8 8 = 1 x_1 = \frac{1 — 7}{8} = -\frac{6}{8} = -\frac{3}{4}, \quad x_2 = \frac{1 + 7}{8} = \frac{8}{8} = 1
Шаг 3: Определим верхнюю функцию
Проверим при x = 0 x = 0 y 1 = 2 ⋅ 0 2 = 0 y_1 = 2 \cdot 0^2 = 0 y 2 = 0.5 ⋅ 0 + 1.5 = 1.5 y_2 = 0.5 \cdot 0 + 1.5 = 1.5 y = 0.5 x + 1.5 y = 0.5x + 1.5
Шаг 4: Разница между функциями
S = ∫ − 3 / 4 1 ( ( 0.5 x + 1.5 ) − 2 x 2 ) d x = ∫ − 3 / 4 1 ( 0.5 x + 1.5 − 2 x 2 ) d x S = \int_{-3/4}^{1} \left( (0.5x + 1.5) — 2x^2 \right) dx = \int_{-3/4}^{1} (0.5x + 1.5 — 2x^2) \, dx
Шаг 5: Интегрируем
∫ ( 0.5 x + 1.5 − 2 x 2 ) d x = 0.5 ⋅ x 2 2 + 1.5 x − 2 ⋅ x 3 3 = 1 4 x 2 + 1.5 x − 2 3 x 3 \int \left( 0.5x + 1.5 — 2x^2 \right) dx = 0.5 \cdot \frac{x^2}{2} + 1.5x — 2 \cdot \frac{x^3}{3} = \frac{1}{4}x^2 + 1.5x — \frac{2}{3}x^3
Шаг 6: Подстановка пределов
В точке x = 1 x = 1
1 4 ( 1 ) 2 + 1.5 ⋅ 1 − 2 3 ⋅ 1 3 = 1 4 + 3 2 − 2 3 \frac{1}{4}(1)^2 + 1.5 \cdot 1 — \frac{2}{3} \cdot 1^3 = \frac{1}{4} + \frac{3}{2} — \frac{2}{3}
В точке x = − 3 4 x = -\frac{3}{4}
x 2 = 9 16 x^2 = \frac{9}{16} x 3 = − 27 64 x^3 = -\frac{27}{64} 1 4 ⋅ 9 16 = 9 64 , 1.5 ⋅ ( − 3 4 ) = − 9 8 , 2 3 ⋅ ( − 27 64 ) = − 54 192 = − 9 32 \frac{1}{4} \cdot \frac{9}{16} = \frac{9}{64}, \quad 1.5 \cdot (-\frac{3}{4}) = -\frac{9}{8}, \quad \frac{2}{3} \cdot \left( -\frac{27}{64} \right) = -\frac{54}{192} = -\frac{9}{32}
Сумма:
9 64 − 9 8 + 9 32 = приведём к общему знаменателю 64: \frac{9}{64} — \frac{9}{8} + \frac{9}{32} = \text{приведём к общему знаменателю 64:} 9 64 − 72 64 + 18 64 = − 45 64 \frac{9}{64} — \frac{72}{64} + \frac{18}{64} = \frac{-45}{64}
Теперь вся площадь:
( 1 4 + 3 2 − 2 3 ) + 45 64 \left( \frac{1}{4} + \frac{3}{2} — \frac{2}{3} \right) + \frac{45}{64}
Приводим к общему знаменателю:
1 4 = 48 192 , 3 2 = 288 192 , 2 3 = 128 192 ⇒ 48 + 288 − 128 192 = 208 192 \frac{1}{4} = \frac{48}{192}, \quad \frac{3}{2} = \frac{288}{192}, \quad \frac{2}{3} = \frac{128}{192} \Rightarrow \frac{48 + 288 — 128}{192} = \frac{208}{192}
Добавляем:
208 192 + 135 192 = 343 192 = 1 151 192 \frac{208}{192} + \frac{135}{192} = \frac{343}{192} = 1 \frac{151}{192}
Ответ:
S = 1 151 192 S = 1 \frac{151}{192}




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!