ГДЗ по Алгебре 10-11 Класс Номер 1014 Алимов — Подробные Ответы

Найти площадь фигуры, ограниченной заданными линиями (1014—1023).

1. параболой у = (х + 1)2, прямой у = 1-х и осью Ох;
2. параболой у = 4-х2, прямой у = х + 2 и осью Ох;
3. параболой у = 4х — х2, прямой у = 4 — х и осью Ох;
4. параболой y = Зх2, прямой у=1,5х + 4,5 и осью Ох.

1) $y = (x + 1)^2$ и $y = 1 — x$;

Точки пересечения функций:

$$(x + 1)^2 = 1 — x;$$ $$x^2 + 2x + 1 — 1 + x = 0;$$ $$x^2 + 3x = 0;$$ $$x \cdot (x + 3) = 0;$$ $$x_1 = 0 \quad \text{и} \quad x_2 = -3;$$

Первая функция:

$$(x + 1)^2 > 0;$$ $$x + 1 \neq 0, \quad \text{отсюда } x \neq -1;$$

Вторая функция:

$$1 — x > 0, \quad \text{отсюда } x < 1;$$

Площадь криволинейной трапеции:

$$S = \int_{-1}^{0} (x + 1)^2 \, dx + \int_{0}^{1} (1 — x) \, dx = \int_{-1}^{0} (x^2 + 2x + 1) \, dx + \int_{0}^{1} (1 — x) \, dx =$$ $$= \left( \frac{x^3}{3} + 2 \cdot \frac{x^2}{2} + 1 \cdot \frac{x^1}{1} \right) \bigg|_{-1}^{0} + \left( 1 \cdot \frac{x^1}{1} — \frac{x^2}{2} \right) \bigg|_{0}^{1} =$$ $$= \left( \frac{x^3}{3} + x^2 + x \right) \bigg|_{-1}^{0} + \left( x — \frac{x^2}{2} \right) \bigg|_{0}^{1} =$$ $$= \frac{0^3}{3} + 0^2 + 0 — \left( \frac{(-1)^3}{3} + (-1)^2 + (-1) \right) + \left( 1 — \frac{1^2}{2} \right) — \left( 0 — \frac{0^2}{2} \right) =$$ $$= \frac{1}{3} + 1 — 1 + \frac{1}{2} = \frac{2}{6} + 1 — \frac{3}{6} = 1 — \frac{1}{6} = \frac{5}{6};$$

Ответ: $\frac{5}{6}$.

2) $y = 4 — x^2$ и $y = x + 2$;

Точки пересечения функций:

$$4 — x^2 = x + 2;$$ $$4 — x^2 — x — 2 = 0;$$ $$x^2 + x — 2 = 0;$$ $$D = 1^2 + 4 \cdot 2 = 1 + 8 = 9, \quad \text{тогда:}$$ $$x_1 = \frac{-1 — 3}{2} = -2 \quad \text{и} \quad x_2 = \frac{-1 + 3}{2} = 1;$$

Первая функция:

$$4 — x^2 > 0;$$ $$x^2 < 4;$$ $$-2 < x < 2;$$

Вторая функция:

$$x + 2 > 0, \quad \text{отсюда } x > -2;$$

Площадь криволинейной трапеции:

$$S = \int_{-2}^{1} (x + 2) \, dx + \int_{1}^{2} (4 — x^2) \, dx = \left( \frac{x^2}{2} + 2 \cdot \frac{x^1}{1} \right) \bigg|_{-2}^{1} + \left( 4 \cdot \frac{x^1}{1} — \frac{x^3}{3} \right) \bigg|_{1}^{2} =$$ $$= \left( \frac{x^2}{2} + 2x \right) \bigg|_{-2}^{1} + \left( 4x — \frac{x^3}{3} \right) \bigg|_{1}^{2} =$$ $$= \frac{1^2}{2} + 2 \cdot 1 — \left( \frac{(-2)^2}{2} + 2 \cdot (-2) \right) + \left( 4 \cdot 2 — \frac{2^3}{3} \right) — \left( 4 \cdot 1 — \frac{1^3}{3} \right) =$$ $$= \frac{1}{2} + 2 — 2 — \frac{8}{3} + 8 — 4 + \frac{1}{3} = 8 + \frac{1}{2} — \frac{7}{3} = \frac{48 + 3 — 14}{6} = \frac{37}{6} = 6 \frac{1}{6};$$

Ответ: $6 \frac{1}{6}$.

3) $y = 4x — x^2$ и $y = 4 — x$;

Точки пересечения функций:

$$4x — x^2 = 4 — x;$$ $$x^2 — x — 4x + 4 = 0;$$ $$x^2 — 5x + 4 = 0;$$ $$D = 5^2 — 4 \cdot 4 = 25 — 16 = 9, \quad \text{тогда:}$$ $$x_1 = \frac{5 — 3}{2} = 1 \quad \text{и} \quad x_2 = \frac{5 + 3}{2} = 4;$$

Первая функция:

$$4x — x^2 > 0;$$ $$x \cdot (4 — x) > 0;$$ $$0 < x < 4;$$

Вторая функция:

$$4 — x > 0, \quad \text{отсюда } x < 4;$$

Площадь криволинейной трапеции:

$$S = \int_{0}^{1} (4x — x^2) \, dx + \int_{1}^{4} (4 — x) \, dx = \left( 4 \cdot \frac{x^2}{2} — \frac{x^3}{3} \right) \bigg|_{0}^{1} + \left( 4 \cdot \frac{x^1}{1} — \frac{x^2}{2} \right) \bigg|_{1}^{4} =$$ $$= \left( 2x^2 — \frac{x^3}{3} \right) \bigg|_{0}^{1} + \left( 4x — \frac{x^2}{2} \right) \bigg|_{1}^{4} =$$ $$= 2 \cdot 1^2 — \frac{1^3}{3} — 2 \cdot 0^2 + \frac{0^3}{3} + 4 \cdot 4 — \frac{4^2}{2} — 4 \cdot 1 + \frac{1^2}{2} =$$ $$= 2 — \frac{1}{3} + 16 — 8 + \frac{1}{2} = 6 — \frac{1}{3} + \frac{1}{2} = \frac{36 — 2 + 3}{6} = \frac{37}{6} = 6 \frac{1}{6};$$

Ответ: $6 \frac{1}{6}$.

4) $y = 3x^2$ и $y = 1,5x + 4,5$;

Точки пересечения функций:

$$3x^2 = 1,5x + 4,5;$$ $$6x^2 — 3x — 9 = 0;$$ $$2x^2 — x — 3 = 0;$$ $$D = 1^2 + 4 \cdot 2 \cdot 3 = 1 + 24 = 25, \quad \text{тогда:}$$ $$x_1 = \frac{1 — 5}{2 \cdot 2} = -1 \quad \text{и} \quad x_2 = \frac{1 + 5}{2 \cdot 2} = \frac{6}{4} = 1,5;$$

Первая функция:

$$3x^2 > 0;$$ $$3x^2 \neq 0, \quad \text{отсюда } x \neq 0;$$

Вторая функция:

$$1,5x + 4,5 > 0;$$ $$1,5x > -4,5, \quad \text{отсюда } x > -3;$$

Площадь криволинейной трапеции:

$$S = \int_{-1}^{0} 3x^2 \, dx + \int_{-3}^{-1} (1.5x + 4.5) \, dx = \left( 3 \cdot \frac{x^3}{3} \right) \bigg|_{-1}^{0} + \left( 1.5 \cdot \frac{x^2}{2} + 4.5 \cdot \frac{x^1}{1} \right) \bigg|_{-3}^{-1} =$$ $$= x^3 \bigg|_{-1}^{0} + \left( \frac{3}{4} x^2 + \frac{9}{2} x \right) \bigg|_{-3}^{-1} =$$ $$= 0^3 — (-1)^3 + \frac{3}{4} \cdot (-1)^2 + \frac{9}{2} \cdot (-1) — \left( \frac{3}{4} \cdot (-3)^2 + \frac{9}{2} \cdot (-3) \right) =$$ $$= 1 + \frac{3}{4} — \frac{9}{2} — \frac{27}{4} + \frac{27}{2} = 1 — \frac{24}{4} + \frac{18}{2} = 1 — 6 + 9 = 4;$$

Ответ: $4$.

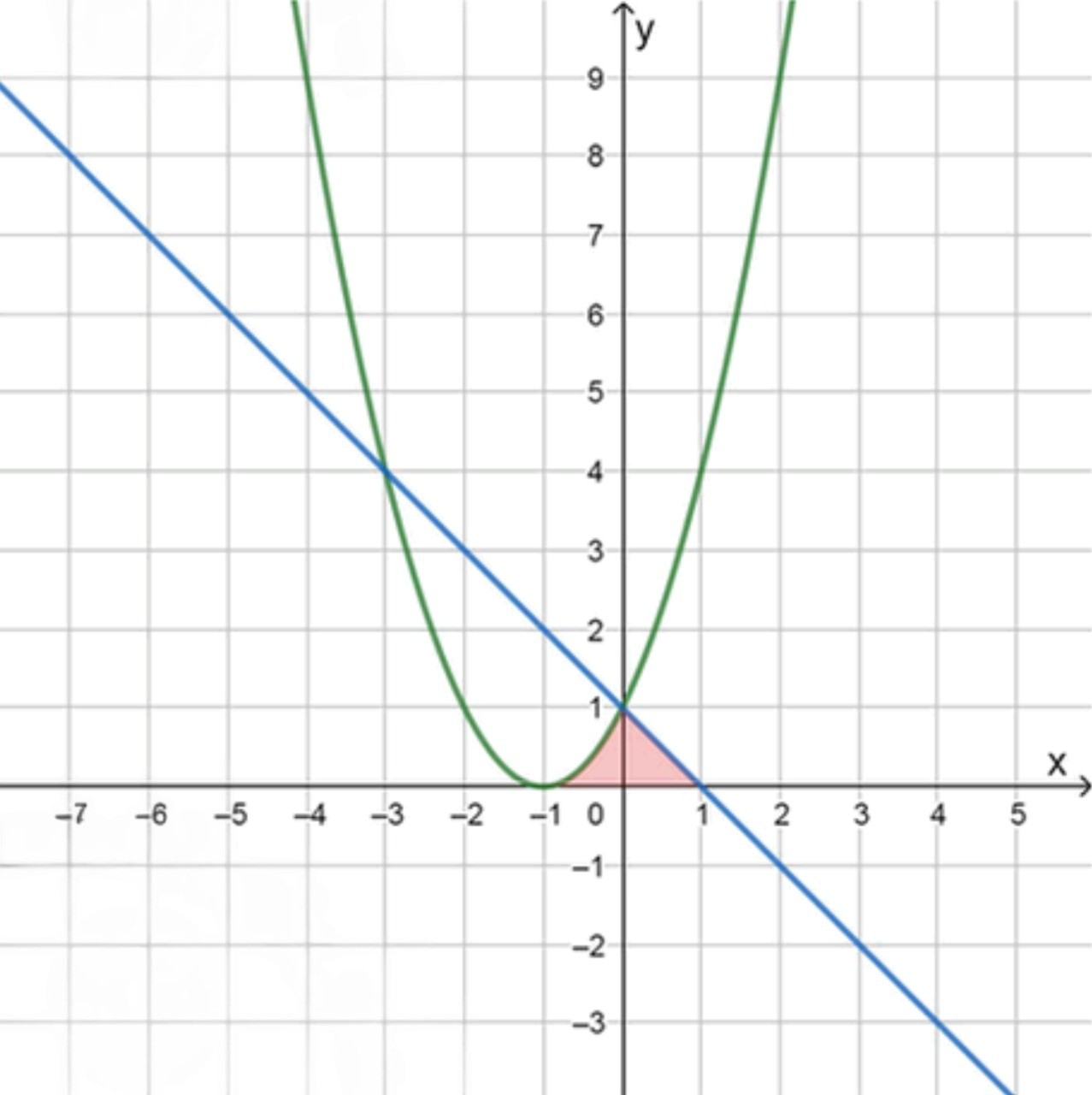
Задача 1: $y = (x + 1)^2$ и $y = 1 — x$

Шаг 1: Найдем точки пересечения:

Решим уравнение:

$$(x + 1)^2 = 1 — x$$

Раскроем скобки:

$$x^2 + 2x + 1 = 1 — x$$

Переносим все на одну сторону:

$$x^2 + 2x + 1 — 1 + x = 0$$ $$x^2 + 3x = 0$$

Вынесем общий множитель:

$$x(x + 3) = 0$$

Отсюда получаем:

$$x_1 = 0 \quad \text{и} \quad x_2 = -3$$

Шаг 2: Обозначим область определения функций:

Первая функция $y = (x + 1)^2$:

$$(x + 1)^2 > 0 \quad \text{для всех } x \neq -1.$$

Вторая функция $y = 1 — x$:

$$1 — x > 0 \quad \Rightarrow \quad x < 1.$$

Шаг 3: Найдем площадь криволинейной трапеции:

Площадь ограничена функциями на интервалах $[-1, 0]$ и $[0, 1]$.

Сначала вычислим два интеграла:

$$S = \int_{-1}^{0} (x + 1)^2 \, dx + \int_{0}^{1} (1 — x) \, dx$$

Раскроем интегралы:

$$\int_{-1}^{0} (x + 1)^2 \, dx = \int_{-1}^{0} (x^2 + 2x + 1) \, dx$$ $$= \left[ \frac{x^3}{3} + x^2 + x \right]_{-1}^{0}$$

Вычислим значения в пределах предела:

$$= \left( \frac{0^3}{3} + 0^2 + 0 \right) — \left( \frac{(-1)^3}{3} + (-1)^2 + (-1) \right) = 0 — \left( -\frac{1}{3} + 1 — 1 \right)$$ $$= 0 + \frac{1}{3} = \frac{1}{3}$$

Теперь для второго интеграла:

$$\int_{0}^{1} (1 — x) \, dx = \left[ x — \frac{x^2}{2} \right]_{0}^{1}$$ $$= \left( 1 — \frac{1^2}{2} \right) — \left( 0 — \frac{0^2}{2} \right) = 1 — \frac{1}{2} = \frac{1}{2}$$

Суммируем полученные площади:

$$S = \frac{1}{3} + \frac{1}{2} = \frac{2}{6} + \frac{3}{6} = \frac{5}{6}$$

Ответ:

$$S = \frac{5}{6}$$

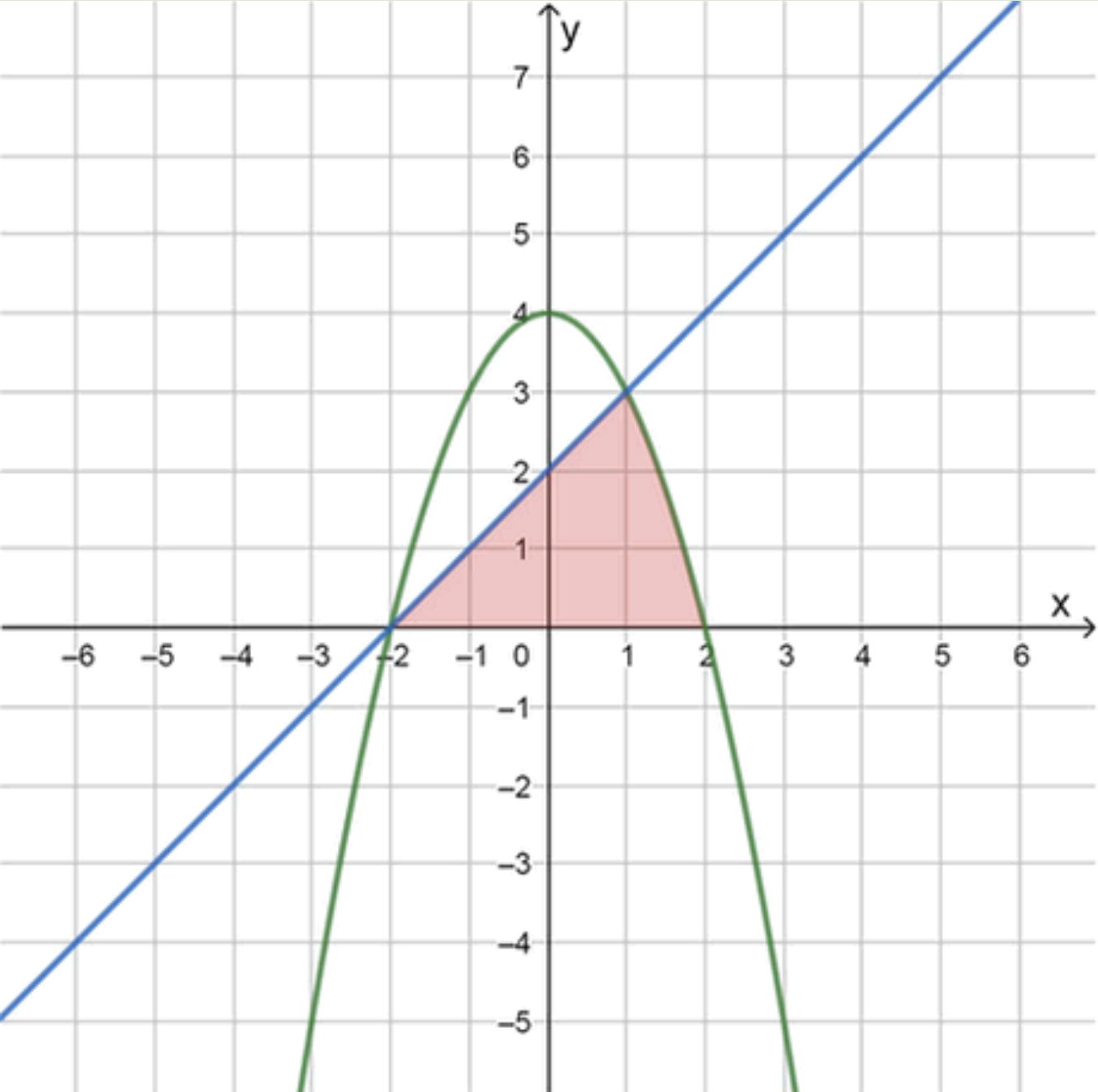
Задача 2: $y = 4 — x^2$ и $y = x + 2$

Шаг 1: Найдем точки пересечения:

Решим уравнение:

$$4 — x^2 = x + 2$$

Переносим все на одну сторону:

$$4 — x^2 — x — 2 = 0$$ $$-x^2 — x + 2 = 0$$

Умножим на -1:

$$x^2 + x — 2 = 0$$

Решаем квадратное уравнение по формуле:

$$D = 1^2 — 4 \cdot 1 \cdot (-2) = 1 + 8 = 9$$ $$x_1 = \frac{-1 — 3}{2} = -2 \quad \text{и} \quad x_2 = \frac{-1 + 3}{2} = 1$$

Шаг 2: Обозначим область определения функций:

Первая функция $y = 4 — x^2$:

$$4 — x^2 > 0 \quad \Rightarrow \quad x^2 < 4 \quad \Rightarrow \quad -2 < x < 2.$$

Вторая функция $y = x + 2$:

$$x + 2 > 0 \quad \Rightarrow \quad x > -2.$$

Шаг 3: Найдем площадь криволинейной трапеции:

Площадь ограничена функциями на интервалах $[-2, 1]$ и $[1, 2]$.

Вычислим два интеграла:

$$S = \int_{-2}^{1} (x + 2) \, dx + \int_{1}^{2} (4 — x^2) \, dx$$

Для первого интеграла:

$$\int_{-2}^{1} (x + 2) \, dx = \left[ \frac{x^2}{2} + 2x \right]_{-2}^{1}$$ $$= \left( \frac{1^2}{2} + 2 \cdot 1 \right) — \left( \frac{(-2)^2}{2} + 2 \cdot (-2) \right) = \left( \frac{1}{2} + 2 \right) — \left( \frac{4}{2} — 4 \right)$$ $$= \frac{5}{2} — \left( 2 — 4 \right) = \frac{5}{2} + 2 = \frac{9}{2}$$

Для второго интеграла:

$$\int_{1}^{2} (4 — x^2) \, dx = \left[ 4x — \frac{x^3}{3} \right]_{1}^{2}$$ $$= \left( 4 \cdot 2 — \frac{2^3}{3} \right) — \left( 4 \cdot 1 — \frac{1^3}{3} \right) = \left( 8 — \frac{8}{3} \right) — \left( 4 — \frac{1}{3} \right)$$ $$= 8 — \frac{8}{3} — 4 + \frac{1}{3} = 4 — \frac{7}{3} = \frac{12}{3} — \frac{7}{3} = \frac{5}{3}$$

Суммируем площади:

$$S = \frac{9}{2} + \frac{5}{3} = \frac{27}{6} + \frac{10}{6} = \frac{37}{6} = 6 \frac{1}{6}$$

Ответ:

$$S = 6 \frac{1}{6}$$

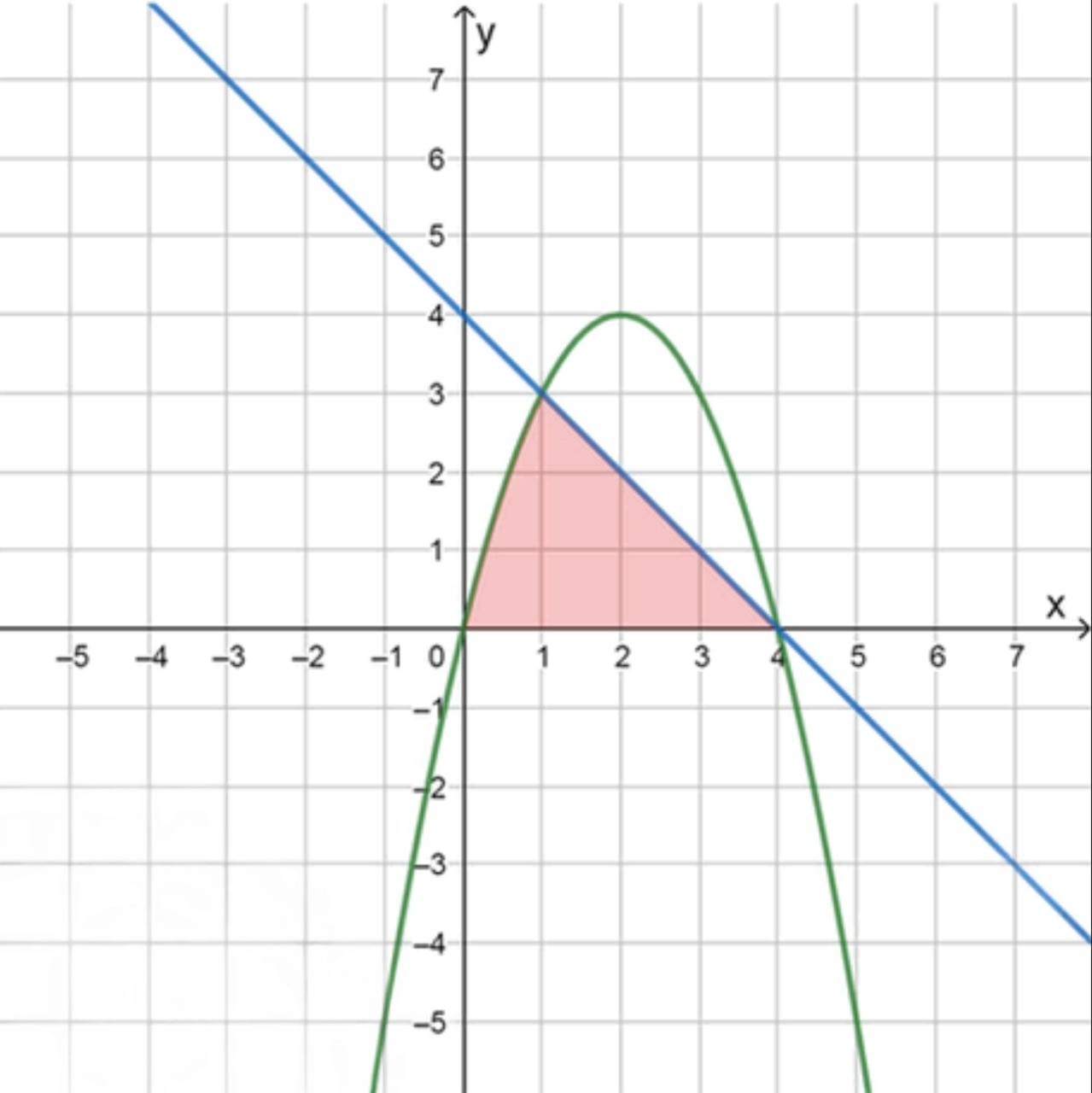
Задача 3: $y = 4x — x^2$ и $y = 4 — x$

Шаг 1: Найдем точки пересечения:

Решим уравнение:

$$4x — x^2 = 4 — x$$

Переносим все на одну сторону:

$$x^2 — x — 4x + 4 = 0$$ $$x^2 — 5x + 4 = 0$$

Дискриминант:

$$D = (-5)^2 — 4 \cdot 1 \cdot 4 = 25 — 16 = 9$$

Решаем уравнение:

$$x_1 = \frac{5 — 3}{2} = 1 \quad \text{и} \quad x_2 = \frac{5 + 3}{2} = 4$$

Шаг 2: Обозначим область определения функций:

Первая функция $y = 4x — x^2$:

$$4x — x^2 > 0 \quad \Rightarrow \quad x(4 — x) > 0 \quad \Rightarrow \quad 0 < x < 4.$$

Вторая функция $y = 4 — x$:

$$4 — x > 0 \quad \Rightarrow \quad x < 4.$$

Шаг 3: Найдем площадь криволинейной трапеции:

Площадь ограничена функциями на интервалах $[0, 1]$ и $[1, 4]$.

Вычислим два интеграла:

$$S = \int_{0}^{1} (4x — x^2) \, dx + \int_{1}^{4} (4 — x) \, dx$$

Для первого интеграла:

$$\int_{0}^{1} (4x — x^2) \, dx = \left[ 4 \cdot \frac{x^2}{2} — \frac{x^3}{3} \right]_{0}^{1}$$ $$= \left( 2x^2 — \frac{x^3}{3} \right)_{0}^{1} = 2 — \frac{1}{3} = \frac{6}{3} — \frac{1}{3} = \frac{5}{3}$$

Для второго интеграла:

$$\int_{1}^{4} (4 — x) \, dx = \left[ 4x — \frac{x^2}{2} \right]_{1}^{4}$$ $$= \left( 4 \cdot 4 — \frac{4^2}{2} \right) — \left( 4 \cdot 1 — \frac{1^2}{2} \right) = \left( 16 — 8 \right) — \left( 4 — \frac{1}{2} \right)$$ $$= 8 — \left( 4 — \frac{1}{2} \right) = 8 — \frac{7}{2} = \frac{16}{2} — \frac{7}{2} = \frac{9}{2}$$

Суммируем площади:

$$S = \frac{5}{3} + \frac{9}{2} = \frac{10}{6} + \frac{27}{6} = \frac{37}{6} = 6 \frac{1}{6}$$

Ответ:

$$S = 6 \frac{1}{6}$$

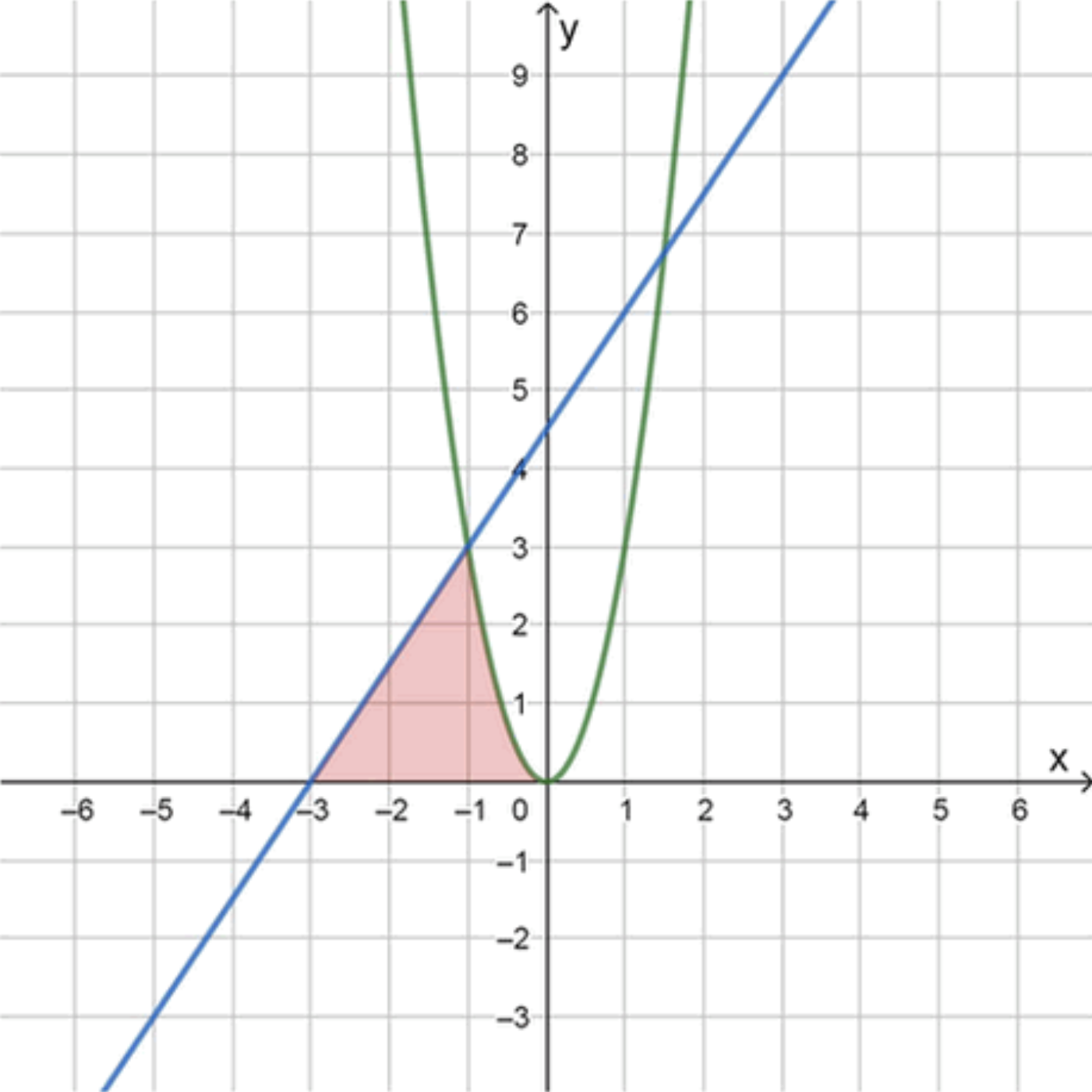
Задача 4: $y = 3x^2$ и $y = 1.5x + 4.5$

Шаг 1: Найдем точки пересечения:

Решим уравнение:

$$3x^2 = 1.5x + 4.5$$

Переносим все на одну сторону:

$$6x^2 — 3x — 9 = 0$$

Разделим на 3:

$$2x^2 — x — 3 = 0$$

Дискриминант:

$$D = (-1)^2 — 4 \cdot 2 \cdot (-3) = 1 + 24 = 25$$

Решаем уравнение:

$$x_1 = \frac{1 — 5}{2 \cdot 2} = -1 \quad \text{и} \quad x_2 = \frac{1 + 5}{2 \cdot 2} = \frac{6}{4} = 1.5$$

Шаг 2: Обозначим область определения функций:

Первая функция $y = 3x^2$:

$$3x^2 > 0 \quad \Rightarrow \quad x \neq 0.$$

Вторая функция $y = 1.5x + 4.5$:

$$1.5x + 4.5 > 0 \quad \Rightarrow \quad x > -3.$$

Шаг 3: Найдем площадь криволинейной трапеции:

Площадь ограничена функциями на интервалах $[-1, 0]$ и $[-3, -1]$.

Вычислим два интеграла:

$$S = \int_{-1}^{0} 3x^2 \, dx + \int_{-3}^{-1} (1.5x + 4.5) \, dx$$

Для первого интеграла:

$$\int_{-1}^{0} 3x^2 \, dx = \left[ x^3 \right]_{-1}^{0} = 0^3 — (-1)^3 = 1$$

Для второго интеграла:

$$\int_{-3}^{-1} (1.5x + 4.5) \, dx = \left[ 1.5 \cdot \frac{x^2}{2} + 4.5x \right]_{-3}^{-1}$$ $$= \left( 1.5 \cdot \frac{(-1)^2}{2} + 4.5 \cdot (-1) \right) — \left( 1.5 \cdot \frac{(-3)^2}{2} + 4.5 \cdot (-3) \right)$$ $$= \left( 0.75 — 4.5 \right) — \left( 6.75 — 13.5 \right) = (-3.75) — (-6.75) = 3$$

Суммируем площади:

$$S = 1 + 3 = 4$$

Ответ:

$$S = 4$$