ГДЗ по Алгебре 10-11 Класс Номер 934 Алимов — Подробные Ответы

Найти число действительных корней уравнения:

1. х4 — 4х3 + 20 = 0;
2. 8х3 — 3х4 — 7 = 0.

Задача 1:

$x^4-4x^3+20=0$;

а) Область определения:
$D(x)=(-\mathrm{\infty };+\mathrm{\infty });$

б) Производная функции:

$$y^{\mathrm{\prime }}(x)=(x^4{)}^{\mathrm{\prime }}-4\cdot (x^3{)}^{\mathrm{\prime }}+(20{)}^{\mathrm{\prime }};$$$$y^{\mathrm{\prime }}(x)=4x^3-4\cdot 3x^2+0=4x^3-12x^2;$$

в) Стационарные точки:

$$4x^3-12x^2=0;$$$$4x^2\cdot (x-3)=0;$$$$x_1=0\text{ и }{x}_2=3;$$

г) Значения функции:

$$f(0)=0^4-4\cdot 0^3+20=20;$$$$f(3)=3^4-4\cdot 3^3+20=81-108+20=-7;$$

д) Промежутки монотонности:

• Возрастает на $(3;+\mathrm{\infty })$;
• Убывает на $(-\mathrm{\infty };0)\cup (0;3)$;
• $x=3$ — точка минимума;

е) Таблица свойств функции:

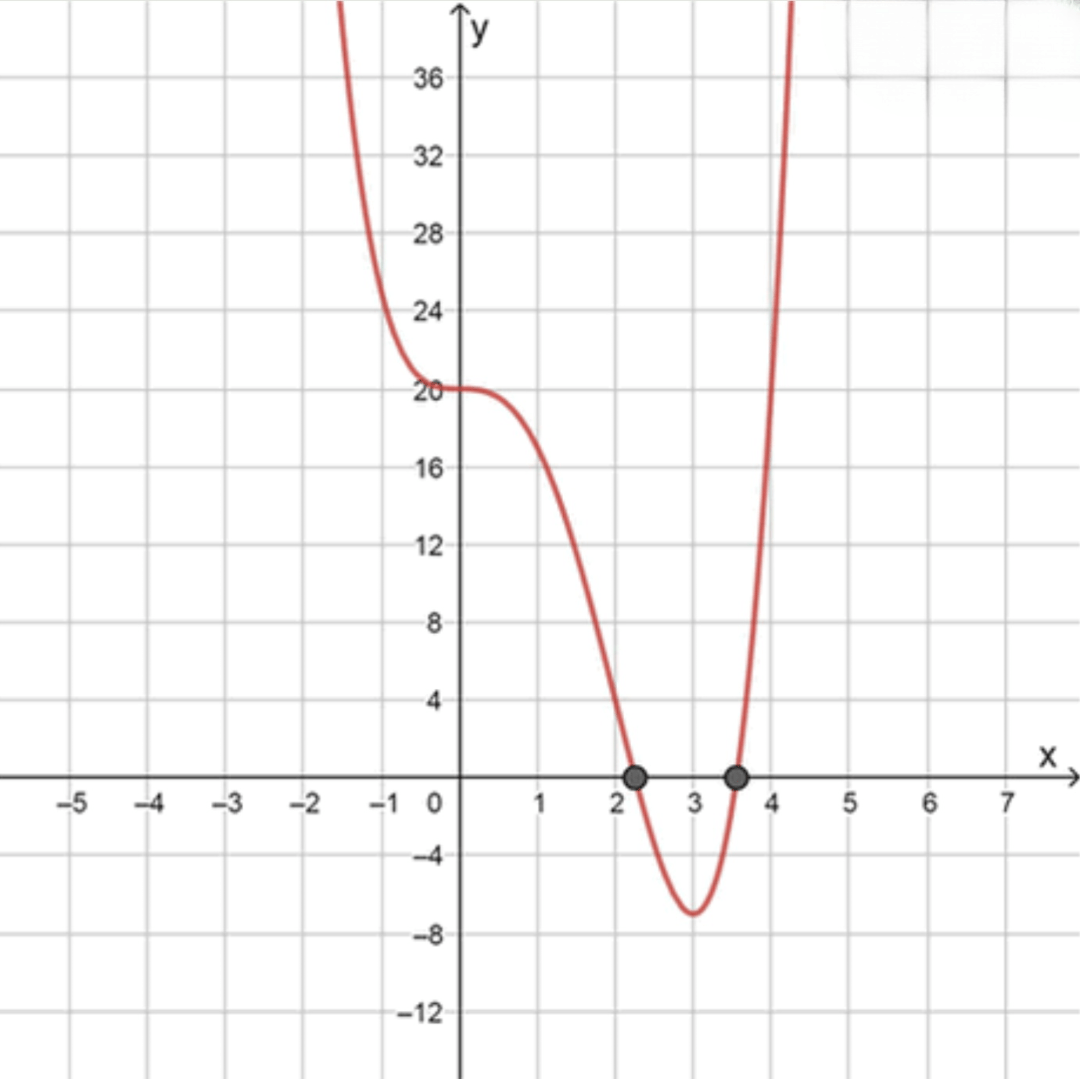
График функции:

Ответ: 2 решения.

Задача 2:

$8x^3-3x^4+7=0$;

а) Область определения:
$D(x)=(-\mathrm{\infty };+\mathrm{\infty });$

б) Производная функции:

$$y^{\mathrm{\prime }}(x)=8\cdot (x^3{)}^{\mathrm{\prime }}-3\cdot (x^4{)}^{\mathrm{\prime }}-(7{)}^{\mathrm{\prime }};$$$$y^{\mathrm{\prime }}(x)=8\cdot 3x^2-3\cdot 4x^3-0=24x^2-12x^3;$$

в) Стационарные точки:

$$24x^2-12x^3=0;$$$$12x^2\cdot (2-x)=0;$$$$x_1=0\text{ и }{x}_2=2;$$

г) Значения функции:

$$f(0)=8\cdot 0^3-3\cdot 0^4+7=-7;$$$$f(2)=8\cdot 2^3-3\cdot 2^4+7=64-48+7=9;$$

д) Промежутки монотонности:

• Возрастает на $(-\mathrm{\infty };0)\cup (0;2)$;
• Убывает на $(2;+\mathrm{\infty })$;
• $x=2$ — точка максимума;

е) Таблица свойств функции:

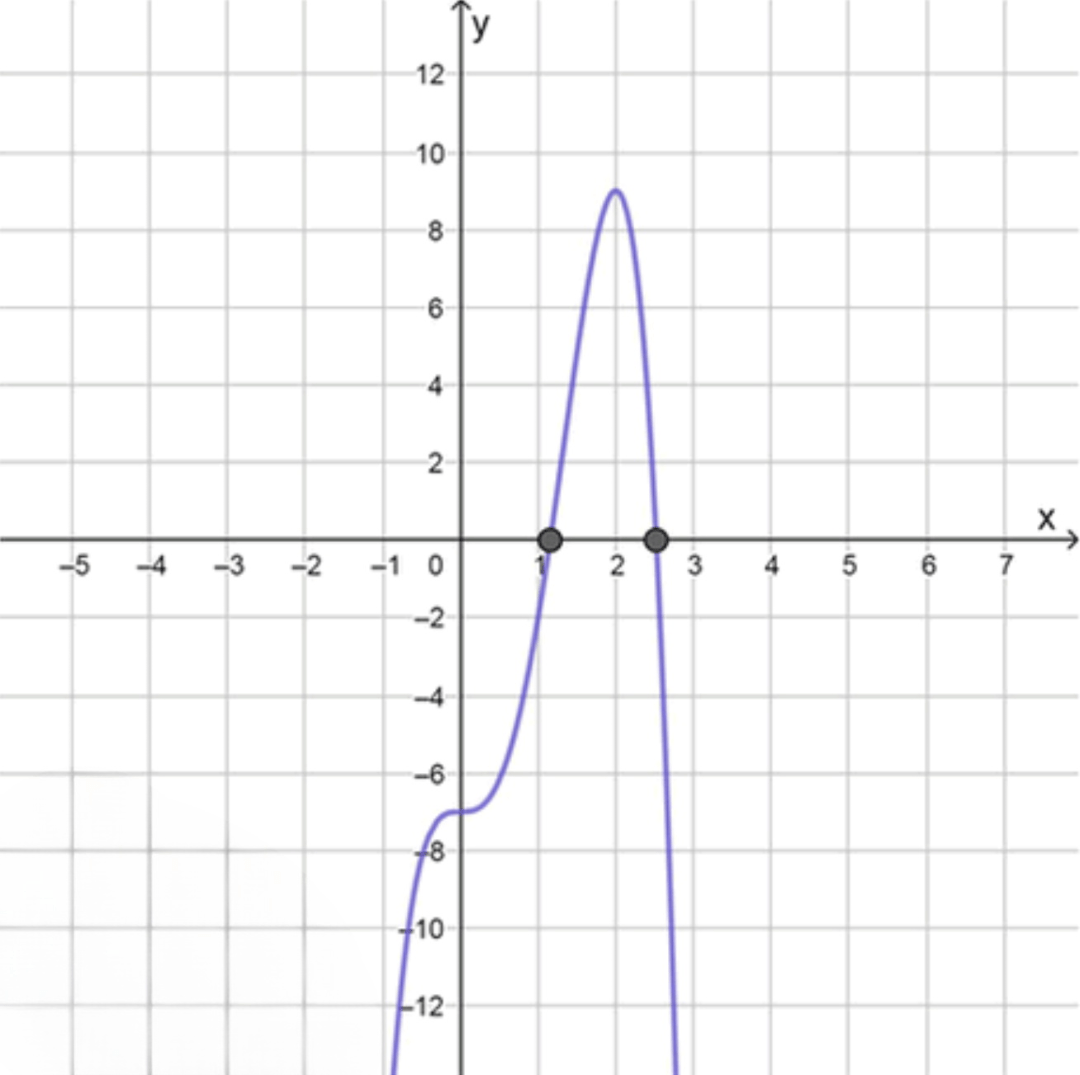
График функции:

Ответ: 2 решения.

Задача 1: $y=x^4-4x^3+20=0$

а) Область определения:

Функция $y=x^4-4x^3+20$ — это многочлен, и многочлены определены на всей числовой прямой. Таким образом, область определения функции:

$$D(x)=(-\mathrm{\infty };+\mathrm{\infty })$$

Ответ:

$$D(x)=(-\mathrm{\infty };+\mathrm{\infty })$$

б) Производная функции:

Нам нужно найти производную функции $y=x^4-4x^3+20$. Для этого применяем стандартные правила дифференцирования для каждого слагаемого:

1. Производная от $x^4$ равна $4x^3$,
2. Производная от $-4x^3$ равна $-12x^2$,
3. Производная от постоянной $20$ равна 0.

Таким образом, производная функции:

$$y^{\mathrm{\prime }}(x)=(x^4{)}^{\mathrm{\prime }}-4\cdot (x^3{)}^{\mathrm{\prime }}+(20{)}^{\mathrm{\prime }}=4x^3-12x^2+0=4x^3-12x^2$$

Ответ:

$$y^{\mathrm{\prime }}(x)=4x^3-12x^2$$

в) Стационарные точки:

Стационарные точки находятся, когда производная функции равна нулю, то есть $y^{\mathrm{\prime }}(x)=0$. Решим уравнение:

$$4x^3-12x^2=0$$

Можно вынести общий множитель $4x^2$:

$$4x^2(x-3)=0$$

Теперь решим это уравнение:

$$4x^2=0\text{или}x-3=0$$

Решения:

$$x_1=0\text{и}{x}_2=3$$

Ответ:
Стационарные точки: $x_1=0$, $x_2=3$

г) Значения функции:

Теперь вычислим значения функции $y=x^4-4x^3+20$ в точках стационарности.

Для $x=0$:

$$f(0)=0^4-4\cdot 0^3+20=20$$

Для $x=3$:

$$f(3)=3^4-4\cdot 3^3+20=81-108+20=-7$$

Ответ:

• $f(0)=20$
• $f(3)=-7$

д) Промежутки монотонности:

Для определения промежутков монотонности нужно исследовать знак производной функции $y^{\mathrm{\prime }}(x)=4x^3-12x^2$. Мы будем учитывать, что знак производной зависит от числителя $4x^2(x-3)$, так как знаменатель всегда положителен.

Для $x<0$:
Подставим $x=-1$:

$$y^{\mathrm{\prime }}(-1)=4(-1{)}^3-12(-1{)}^2=-4-12=-16$$

Это отрицательное значение говорит, что функция убывает на интервале $(-\mathrm{\infty };0)$.

Для $0<x<3$:
Подставим $x=1$:

$$y^{\mathrm{\prime }}(1)=4(1{)}^3-12(1{)}^2=4-12=-8$$

Это отрицательное значение говорит, что функция убывает на интервале $(0;3)$.

Для $x>3$:
Подставим $x=4$:

$$y^{\mathrm{\prime }}(4)=4(4{)}^3-12(4{)}^2=4\cdot 64-12\cdot 16=256-192=64$$

Это положительное значение говорит, что функция возрастает на интервале $(3;+\mathrm{\infty })$.

Ответ:

• Функция возрастает на $(3;+\mathrm{\infty })$
• Функция убывает на $(-\mathrm{\infty };0)\cup (0;3)$
• $x=3$ — точка минимума
• $x=0$ — точка максимума

е) Таблица свойств функции:

Задача 2: $8x^3-3x^4+7=0$

а) Область определения:

Функция $y=8x^3-3x^4+7$ также является многочленом, а значит, она определена на всей числовой прямой. Следовательно, область определения функции:

$$D(x)=(-\mathrm{\infty };+\mathrm{\infty })$$

Ответ:

$$D(x)=(-\mathrm{\infty };+\mathrm{\infty })$$

б) Производная функции:

Для нахождения производной функции $y=8x^3-3x^4+7$ используем правила дифференцирования:

1. Производная от $8x^3$ равна $24x^2$,
2. Производная от $-3x^4$ равна $-12x^3$,
3. Производная от постоянной $7$ равна 0.

Итак, производная функции:

$$y^{\mathrm{\prime }}(x)=24x^2-12x^3$$

Ответ:

$$y^{\mathrm{\prime }}(x)=24x^2-12x^3$$

в) Стационарные точки:

Стационарные точки находятся, когда производная функции равна нулю:

$$24x^2-12x^3=0$$

Вынесем общий множитель $12x^2$:

$$12x^2(2-x)=0$$

Решения:

$$x_1=0\text{и}{x}_2=2$$

Ответ:
Стационарные точки: $x_1=0$, $x_2=2$

г) Значения функции:

Теперь подставим найденные стационарные точки в исходную функцию.

Для $x=0$:

$$f(0)=8\cdot 0^3-3\cdot 0^4+7=7$$

Для $x=2$:

$$f(2)=8\cdot 2^3-3\cdot 2^4+7=64-48+7=23$$

Ответ:

• $f(0)=7$
• $f(2)=23$

д) Промежутки монотонности:

Для анализа промежутков монотонности изучим знак производной $y^{\mathrm{\prime }}(x)=24x^2-12x^3$.

Для $x<0$:
Подставим $x=-1$:

$$y^{\mathrm{\prime }}(-1)=24(-1{)}^2-12(-1{)}^3=24+12=36>0$$

Функция возрастает на интервале $(-\mathrm{\infty };0)$.

Для $0<x<2$:
Подставим $x=1$:

$$y^{\mathrm{\prime }}(1)=24(1{)}^2-12(1{)}^3=24-12=12>0$$

Функция возрастает на интервале $(0;2)$.

Для $x>2$:
Подставим $x=3$:

$$y^{\mathrm{\prime }}(3)=24(3{)}^2-12(3{)}^3=216-324=-108<0$$

Функция убывает на интервале $(2;+\mathrm{\infty })$.

Ответ:

• Возрастает на $(-\mathrm{\infty };0)\cup (0;2)$
• Убывает на $(2;+\mathrm{\infty })$
• $x=2$ — точка максимума

е) Таблица свойств функции: