ГДЗ по Алгебре 10-11 Класс Номер 804 Алимов — Подробные Ответы

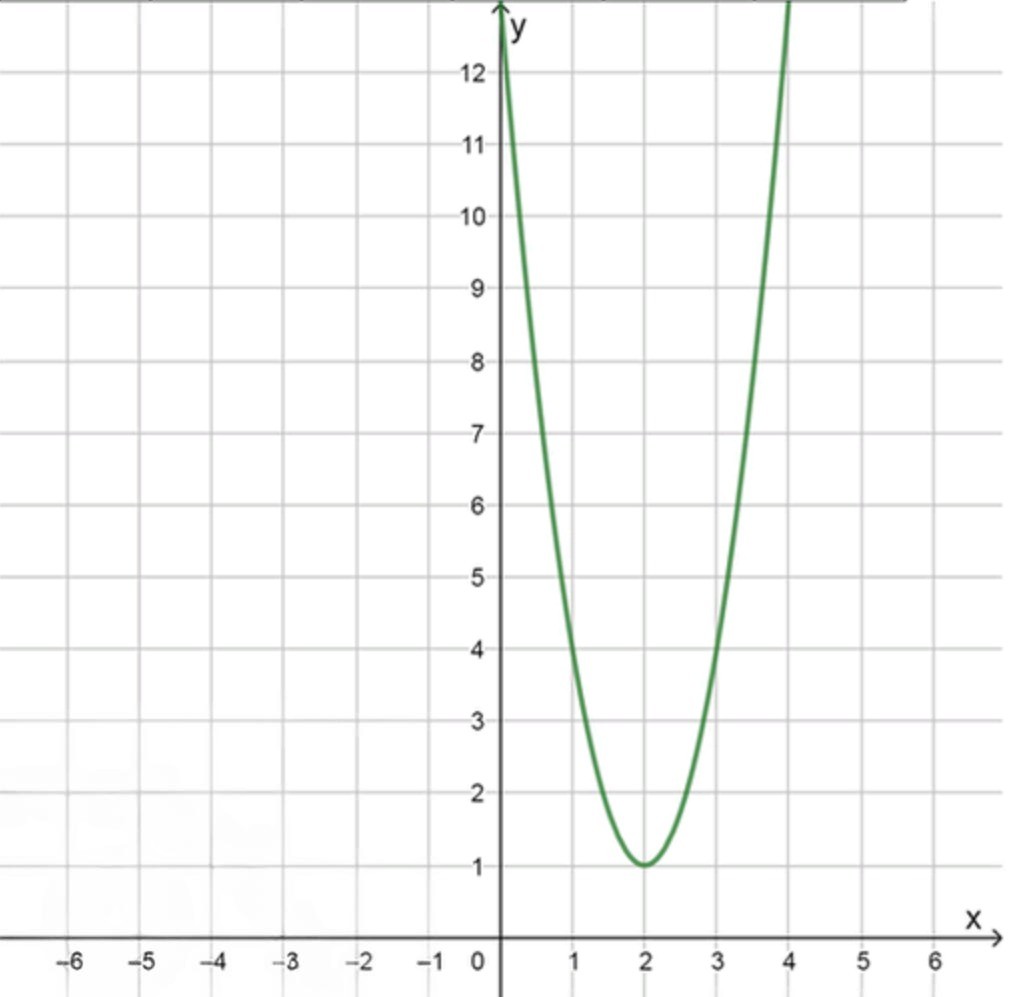
Построить график функции у = 3 (х — 2)2 + 1 и график функции, являющейся её производной.

$y = 3(x — 2)^2 + 1$;
$y = 3(x^2 — 4x + 4) + 1 = 3x^2 — 12x + 12 + 1 = 3x^2 — 12x + 13$;
$y’ = 3 \cdot (x^2)’ — (12x — 13)’ = 3 \cdot 2x — 12 = 6x — 12$;

График функции:
$y = 3x^2 — 12x + 13$;

График производной функции:
$y’ = 6x — 12$;

У нас есть функция:

$$y = 3(x — 2)^2 + 1$$

Наша цель — раскрыть скобки, найти производную функции и построить таблицы для значений функции и её производной.

1. Раскрытие скобок

Для начала раскроем скобки в уравнении функции:

$$y = 3(x — 2)^2 + 1$$

Первым шагом необходимо разложить квадрат бинома:

$$(x — 2)^2 = x^2 — 4x + 4$$

Теперь подставим это выражение в исходное уравнение:

$$y = 3(x^2 — 4x + 4) + 1$$

Далее распределим множитель $3$ по каждому из слагаемых в скобках:

$$y = 3x^2 — 12x + 12 + 1$$

Теперь у нас получается:

$$y = 3x^2 — 12x + 13$$

Таким образом, функция в раскрытом виде:

$$y = 3x^2 — 12x + 13$$

2. Нахождение производной функции

Теперь, когда у нас есть явное выражение для функции $y$, найдём её производную $y’$.

Используем стандартные правила дифференцирования:

• Производная от $x^2$ — это $2x$.
• Производная от $x$ — это 1.
• Производная от постоянной (в данном случае $13$) — это 0.

Дифференцируем $y = 3x^2 — 12x + 13$:

$$y’ = \frac{d}{dx}(3x^2) — \frac{d}{dx}(12x) + \frac{d}{dx}(13)$$

Проводим дифференцирование по каждому члену:

$$y’ = 3 \cdot 2x — 12 \cdot 1 + 0$$

Приводим к более компактному виду:

$$y’ = 6x — 12$$

Таким образом, производная функции:

$$y’ = 6x — 12$$

3. Построение таблиц значений функции и её производной

Теперь построим таблицы значений для функции $y = 3x^2 — 12x + 13$ и её производной $y’ = 6x — 12$.

3.1 Таблица значений функции $y = 3x^2 — 12x + 13$

Для различных значений $x$ подставим их в уравнение функции $y = 3x^2 — 12x + 13$ и получим значения функции $y$.

Рассчитаем для каждого значения $x$:

• Для $x = 0$:

  $$y = 3(0)^2 — 12(0) + 13 = 13$$

• Для $x = 1$:

  $$y = 3(1)^2 — 12(1) + 13 = 3 — 12 + 13 = 4$$

• Для $x = 2$:

  $$y = 3(2)^2 — 12(2) + 13 = 12 — 24 + 13 = 1$$

• Для $x = 3$:

  $$y = 3(3)^2 — 12(3) + 13 = 27 — 36 + 13 = 4$$

• Для $x = 4$:

  $$y = 3(4)^2 — 12(4) + 13 = 48 — 48 + 13 = 13$$

Получаем таблицу значений функции $y$:

3.2 Таблица значений производной $y’ = 6x — 12$

Теперь для различных значений $x$ подставим их в уравнение производной $y’ = 6x — 12$ и получим значения производной.

Рассчитаем для каждого значения $x$:

• Для $x = 1$:

  $$y’ = 6(1) — 12 = 6 — 12 = -6$$

• Для $x = 2$:

  $$y’ = 6(2) — 12 = 12 — 12 = 0$$

Получаем таблицу значений производной $y’$:

Ответ:

• Функция $y = 3x^2 — 12x + 13$.
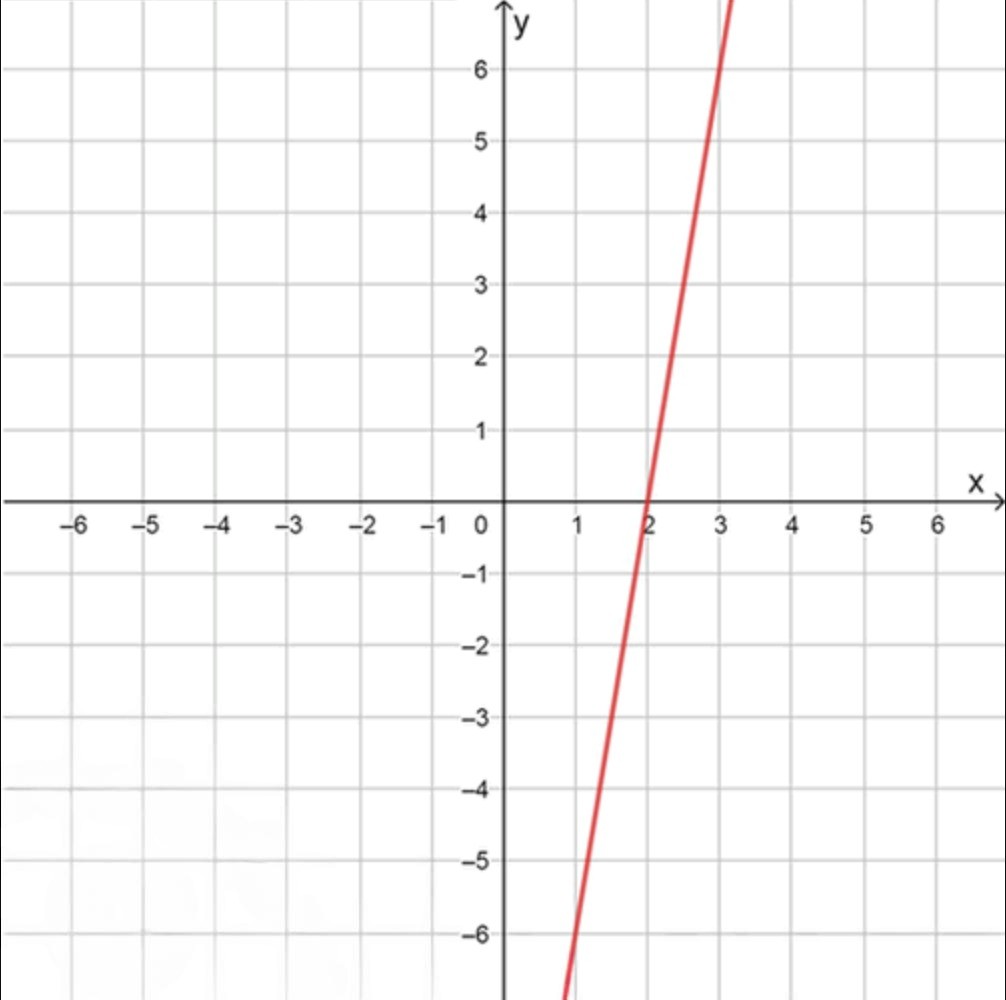
• Производная функции $y’ = 6x — 12$.
• Таблица значений функции:
  

  $x$	0	1	2	3	4
  $y$	13	4	1	4	13

• Таблица значений производной:
  

  $x$	1	2
  $y’$	-6	0