ГДЗ по Алгебре 10-11 Класс Номер 794 Алимов — Подробные Ответы

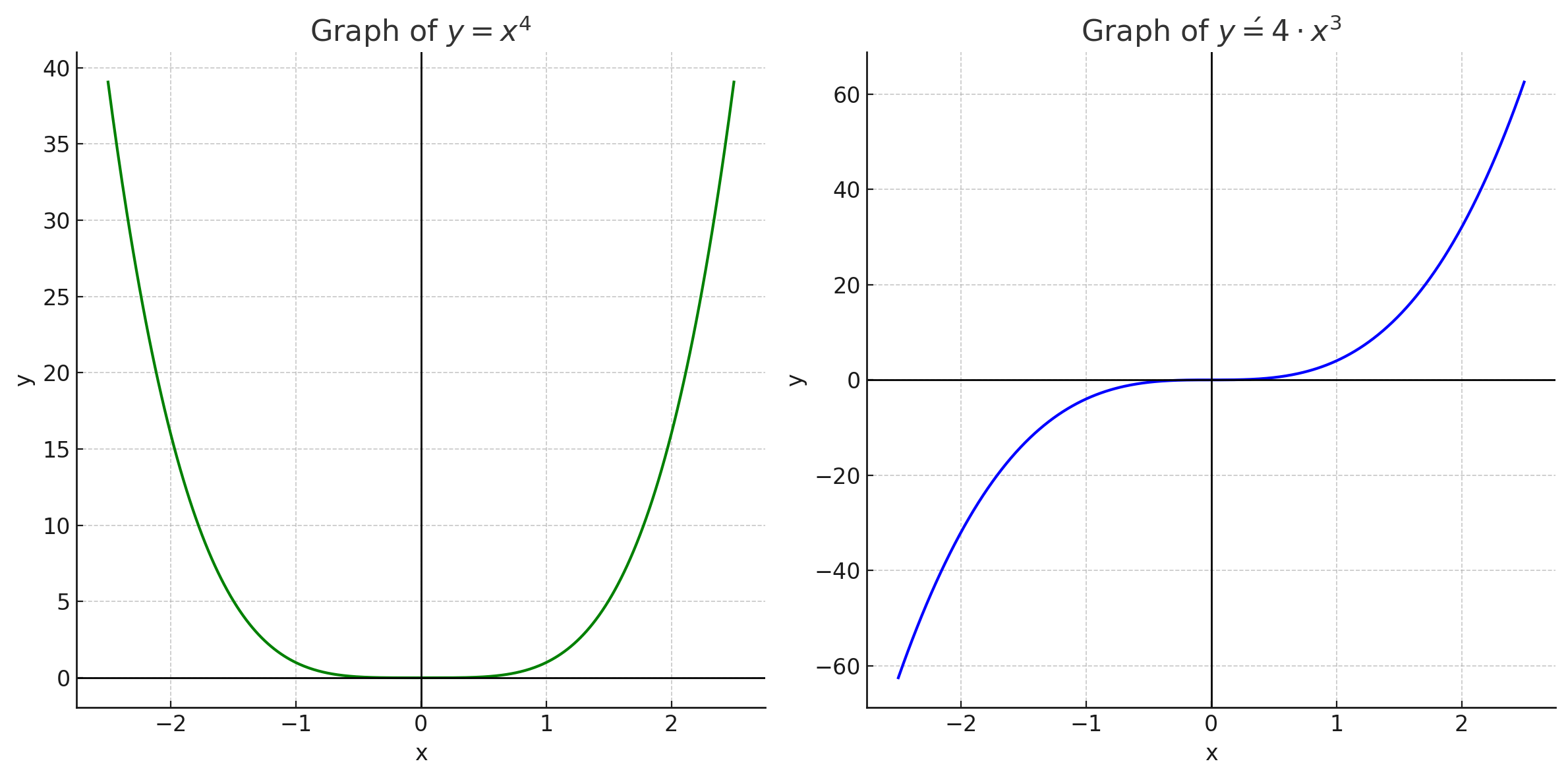
Построить график функции у = х4 и график функции, являющейся её производной.

График функции:

$y = x^4$

$$\begin{array}{|c|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 1 & 2 \\ \hline y & 16 & 1 & 0 & 1 & 16 \\ \hline \end{array}$$

График производной функции:

$y’ = 4 \cdot x^4 — 1 = 4x^3$

$$\begin{array}{|c|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 1 & 2 \\ \hline y & -32 & -4 & 0 & 4 & 32 \\ \hline \end{array}$$

1. График функции $y = x^4$

1.1. Описание функции
Функция $y = x^4$ — это степенная функция с четной степенью. Ключевыми свойствами такой функции являются:

• Функция симметрична относительно оси $y$, то есть она четная ($f(-x) = f(x)$).
• При $x = 0$ значение функции равно нулю, то есть $y = 0$.
• При увеличении или уменьшении $x$, значение функции увеличивается на очень большой и резкий угол, поскольку $x^4$ растёт быстрее, чем квадратичная функция.

1.2. Таблица значений
Таблица значений для функции $y = x^4$ при заданных значениях $x$:

$$\begin{array}{|c|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 1 & 2 \\ \hline y & 16 & 1 & 0 & 1 & 16 \\ \hline \end{array}$$

• Для $x = -2$, $y = (-2)^4 = 16$.
• Для $x = -1$, $y = (-1)^4 = 1$.
• Для $x = 0$, $y = 0^4 = 0$.
• Для $x = 1$, $y = 1^4 = 1$.
• Для $x = 2$, $y = 2^4 = 16$.

1.3. Построение графика
Для построения графика функции на координатной плоскости мы начинаем с точек, соответствующих значениям из таблицы:

• Точка $(-2, 16)$
• Точка $(-1, 1)$
• Точка $(0, 0)$
• Точка $(1, 1)$
• Точка $(2, 16)$

График будет симметричен относительно оси $y$, так как функция четная.

1.4. Анализ графика
График функции $y = x^4$ имеет форму параболы, которая «открывается вверх». Вблизи $x = 0$ функция ведет себя как $y \approx 0$, а при увеличении по модулю $|x|$ функция растет очень быстро.

2. График производной функции $y’ = 4x^3$

2.1. Описание производной
Производная функции $y = x^4$ равна $y’ = 4x^3$. Это кубическая функция, и ее свойства:

• Функция нечётная, то есть она симметрична относительно начала координат: $f(-x) = -f(x)$.
• Для значений $x$ близких к нулю, функция меняет знак на противоположный с учётом степени.

2.2. Таблица значений производной
Таблица значений для производной функции $y’ = 4x^3$ при заданных значениях $x$:

$$\begin{array}{|c|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 1 & 2 \\ \hline y & -32 & -4 & 0 & 4 & 32 \\ \hline \end{array}$$

• Для $x = -2$, $y’ = 4(-2)^3 = -32$.
• Для $x = -1$, $y’ = 4(-1)^3 = -4$.
• Для $x = 0$, $y’ = 4(0)^3 = 0$.
• Для $x = 1$, $y’ = 4(1)^3 = 4$.
• Для $x = 2$, $y’ = 4(2)^3 = 32$.

2.3. Построение графика производной
Точки, соответствующие значениям производной:

• Точка $(-2, -32)$
• Точка $(-1, -4)$
• Точка $(0, 0)$
• Точка $(1, 4)$
• Точка $(2, 32)$

График будет иметь форму кубической функции и пересечет ось $x$ в точке $x = 0$.

2.4. Анализ графика производной

• График функции производной $y’ = 4x^3$ пересекает ось $x$ в точке $x = 0$, где наклон касательной к графику $y = x^4$ равен нулю.
• График функции $y’ = 4x^3$ имеет симметрию относительно начала координат. Для $x > 0$ функция растет, а для $x < 0$ — убывает.
• График функции возрастает при $x > 0$ и убывает при $x < 0$.

3. Соотношение между графиками

График функции $y = x^4$ показывает, как изменяется сама функция, а график производной $y’ = 4x^3$ показывает скорость изменения функции в каждой точке.

• Когда производная равна нулю, это означает, что на графике функции $y = x^4$ есть точка экстремума. В данном случае это минимум в точке $x = 0$.
• График производной помогает увидеть, где функция $y = x^4$ возрастает или убывает. Для $x > 0$ функция возрастает, а для $x < 0$ также возрастает, но с отрицательными значениями наклона.

4. Выводы

• График функции $y = x^4$ имеет форму параболы, которая «открывается вверх».
• График производной $y’ = 4x^3$ показывает, как наклон этой параболы меняется. В точке $x = 0$ наклон равен нулю, что соответствует минимуму функции.