
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 769 Алимов — Подробные Ответы
Решить графически уравнение:
- cosx = |x|;
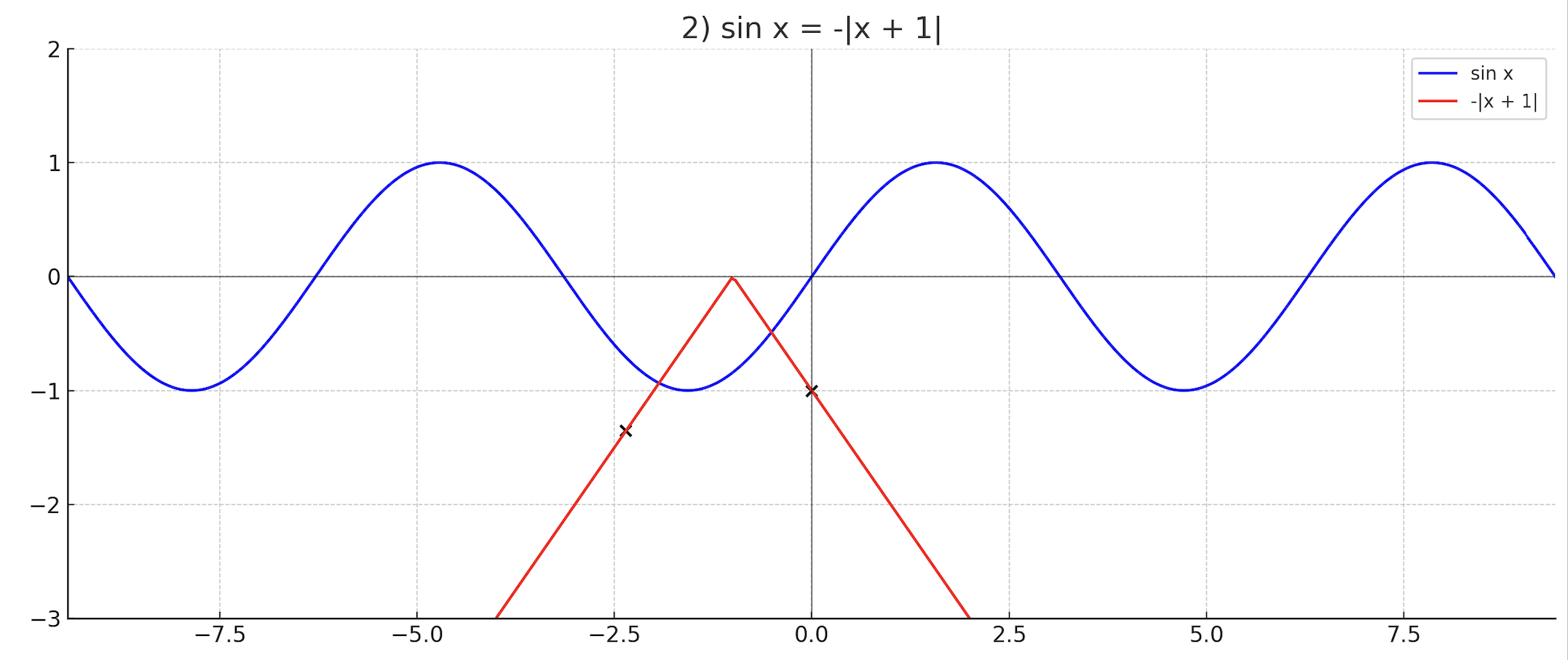
- sinx = -|x +1|.
;
— график модуля:
и ;
Графики функций:
Ответ: 2 решения.
;
— график модуля:
и ;
Графики функций:
Ответ: 2 решения.
Часть 1) Решить уравнение
Шаг 1. Понимание задачи
Нужно найти все значения , при которых значение косинуса равно абсолютному значению , то есть:
Шаг 2. Область определения и свойства функций
- Функция — периодическая, принимает значения от до .
- Функция — модуль числа , принимает только неотрицательные значения и монотонно возрастает по модулю от нуля.
- Значит, правая часть , а левая часть ограничена между и .
Шаг 3. Анализ уравнения
- Так как , а , возможные решения могут быть только там, где , иначе правая часть будет больше, чем максимум левой.
- Следовательно, .
Шаг 4. Построение графиков функций
- График — волнообразная кривая, максимум 1 в точке .
- График — «V»-образная линия, проходящая через начало координат (0,0).
Шаг 5. Точки пересечения графиков
- При , , — не совпадает, значит не решение.
- При , , что больше 1, а — не равны.
- Однако, из таблицы и графика видно, что точки пересечения находятся примерно в точках, где .
- Визуально и численно из графика видно 2 решения в области около .
Шаг 6. Табличные значения
| 0 | |||
|---|---|---|---|
| (y = | x | ) | 0 |
Эти точки — контрольные, показывают значения функции модуля. Решения лежат между и этими значениями.
Шаг 7. Вывод по первой части
- Функции пересекаются в двух точках.
- Ответ: 2 решения.
Часть 2) Решить уравнение
Шаг 1. Понимание задачи
Нужно найти все значения , при которых:
Шаг 2. Анализ функций
- Левая часть — синус, , периодическая функция.
- Правая часть — отрицательное модульное выражение, всегда , и равно 0 только при .
- Значит решения возможны только там, где , то есть синус отрицателен или равен нулю.
- Правая часть убывает при удалении от точки .
Шаг 3. Построение графиков
- График — волнообразный, проходит через (0,0).
- График — перевернутая «V»-образная линия с вершиной в точке .
Шаг 4. Табличные значения
| (y = — | x + 1 | ) | 0 |
Шаг 5. Точки пересечения
- Вершина модуля в точке совпадает с .
- Решения находятся в двух точках, где графики пересекаются (примерно около и ).
- Из графика видно, что таких точек две.
Шаг 6. Вывод по второй части
- Количество решений: 2.
Итог:
- В обоих уравнениях по 2 решения.
- Ответы совпадают с графическим анализом.


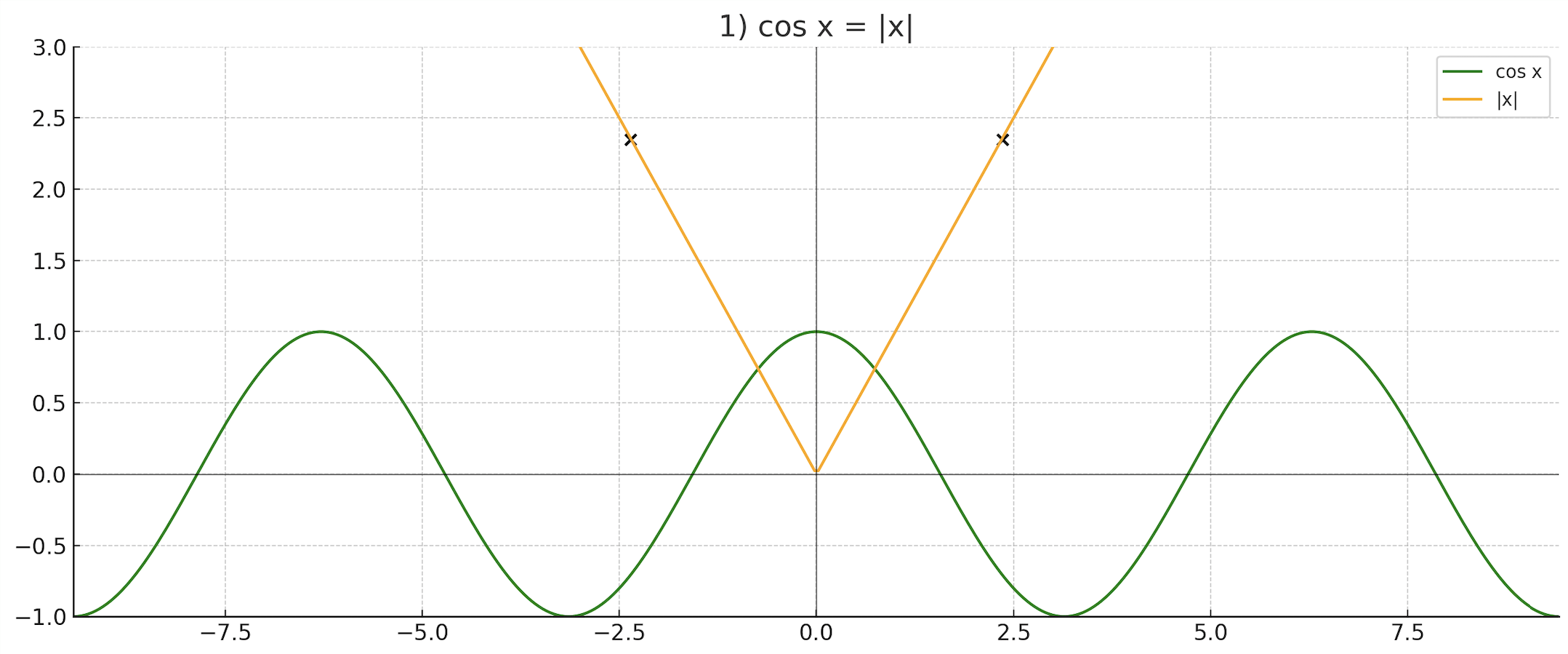

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!