ГДЗ по Алгебре 10-11 Класс Номер 764 Алимов — Подробные Ответы

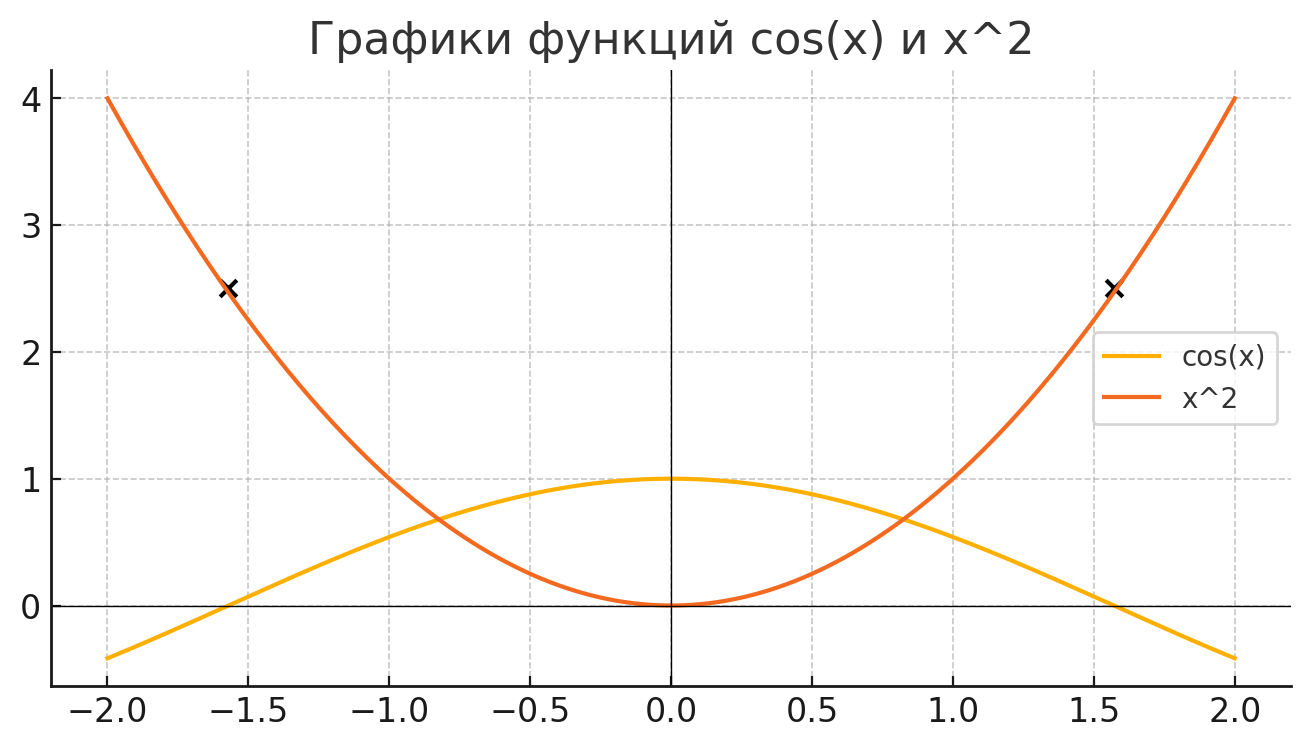
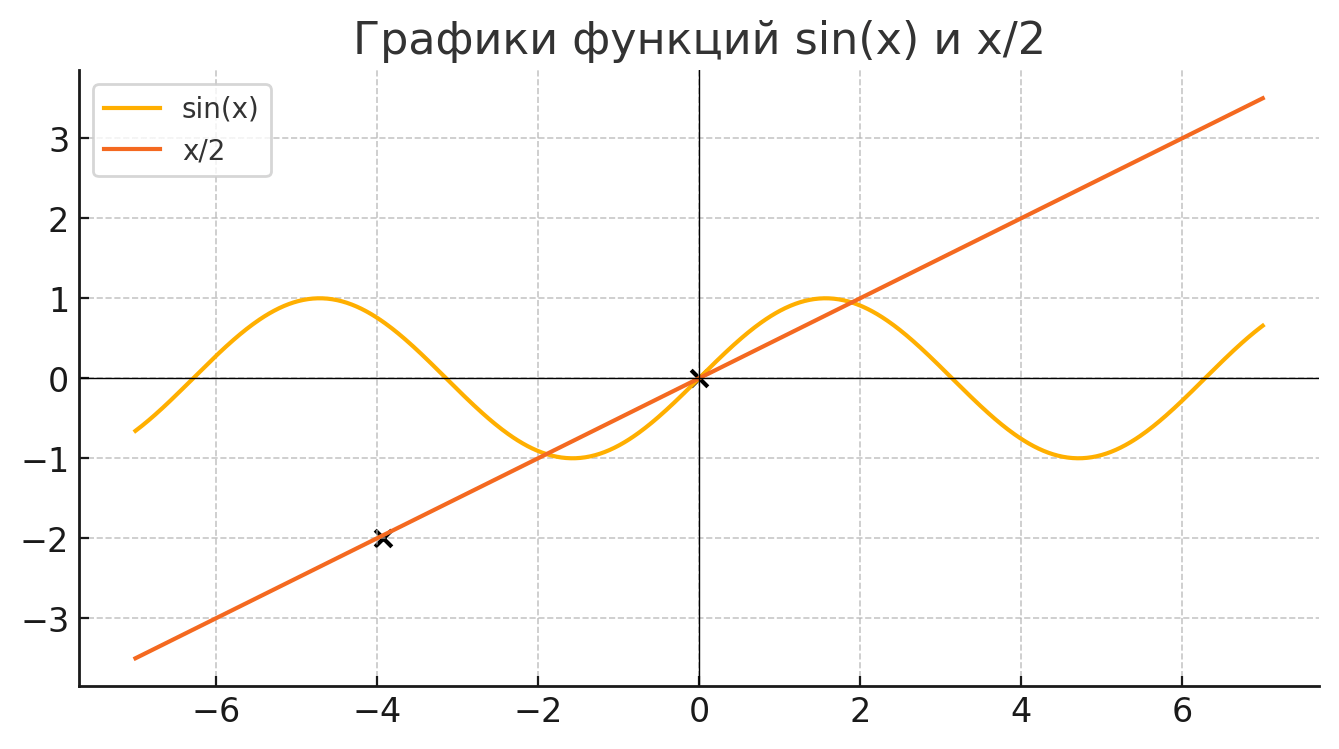
Используя графики, найти число корней уравнения:

1. cosx=x2;
2. sinx=x/2.

$$\[ 1)\cos x=x^2; \]$$

$$\mathrm{}$$ $$y=x^2\text{—}\text{парабола ветвями вверх:}$$

$$y = x^2 \quad — \quad \text{парабола ветвями вверх:}$$ $$\overline{)\begin{array}{cccc}x& 0& -\frac{\pi }{2}& \frac{\pi }{2}\end{array}}$$

$$\overline{)\begin{array}{cccc}y& 0& 2,5& 2,5\end{array}}$$

$$\begin{array}{|c|c|c|c|} \hline x & 0 & -\frac{\pi}{2} & \frac{\pi}{2} \\ \hline y & 0 & 2,5 & 2,5 \\ \hline \end{array}$$ $$\text{Графики функций:}$$

$$\text{Графики функций:}$$ $$\text{Ответ: 2 решения.}$$

$$2)\sin x=\frac{x}{2};$$

$$2) \quad \sin x = \frac{x}{2};$$ $$y=\frac{x}{2}\text{—}\text{прямая:}$$

$$y = \frac{x}{2} \quad — \quad \text{прямая:}$$ $$\overline{)\begin{array}{ccc}x& 0& -\frac{5\pi }{4}\end{array}}$$

$$\overline{)\begin{array}{ccc}y& 0& -2\end{array}}$$

$$\begin{array}{|c|c|c|} \hline x & 0 & -\frac{5\pi}{4} \\ \hline y & 0 & -2 \\ \hline \end{array}$$ $$\text{Графики функций:}$$

$$\text{Графики функций:}$$ $$\text{Ответ: 3 решения.}$$

Задача 1: Решить уравнение $\cos x = x^2$

Шаг 1. Анализ уравнения

Дано уравнение:

$$\cos x = x^2.$$

Правая часть — функция $y = x^2$ — это парабола с ветвями, направленными вверх, у которой вершина в начале координат $(0,0)$. Значения $x^2$ всегда неотрицательны.

Левая часть — функция $y = \cos x$ — колебательная функция с периодом $2\pi$, значения которой лежат в диапазоне $[-1, 1]$.

Шаг 2. Область определения и возможные значения $x$

Поскольку $x^2 \geq 0$, а $\cos x \in [-1, 1]$, уравнение $\cos x = x^2$ возможно только тогда, когда:

$$0 \leq x^2 \leq 1.$$

То есть:

$$-1 \leq x \leq 1.$$

Для больших $|x|$, например, $|x| > 1$, $x^2 > 1$, а $\cos x$ максимум 1, поэтому решения вне $[-1,1]$ невозможны.

Шаг 3. Графический анализ

Построим графики функций:

• $y = \cos x$ — колебательная кривая.
• $y = x^2$ — парабола.

Обозначим точки пересечения графиков.

В таблице приведены значения в ключевых точках:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & -\frac{\pi}{2} & \frac{\pi}{2} \\ \hline y = x^2 & 0 & \left(\frac{\pi}{2}\right)^2 \approx 2.5 & \left(\frac{\pi}{2}\right)^2 \approx 2.5 \\ \hline y = \cos x & 1 & 0 & 0 \\ \hline \end{array}$$

Из таблицы видно, что:

• В точке $x=0$: $\cos 0 = 1$, $0^2=0$, значения не равны.
• В точках $x = \pm \frac{\pi}{2}$, $x^2 \approx 2.5$, $\cos x = 0$.

Шаг 4. Проверка количества решений

Поскольку парабола $y = x^2$ растёт быстро и $\cos x$ колеблется, они могут пересекаться в нескольких точках.

Из графика видно, что есть ровно 2 точки пересечения:

• Одна в отрицательной части отрезка $[-1,0]$.
• Вторая — в положительной части отрезка $[0,1]$.

Это и есть решения уравнения $\cos x = x^2$.

Итог:

$$\boxed{ \text{Уравнение } \cos x = x^2 \text{ имеет } 2 \text{ решения.} }$$

Задача 2: Решить уравнение $\sin x = \frac{x}{2}$

Шаг 1. Анализ уравнения

Дано:

$$\sin x = \frac{x}{2}.$$

Правая часть — линейная функция $y = \frac{x}{2}$.

Левая часть — $y = \sin x$ — периодическая функция с диапазоном значений $[-1, 1]$.

Шаг 2. Область определения и возможные значения

Правая часть растёт линейно без ограничения, а левая часть ограничена.

Рассмотрим, где решения возможны.

Для больших $|x|$:

• Левая часть $\sin x$ ограничена по модулю 1.
• Правая часть растёт без ограничения.

Значит, решения могут быть только при таких $x$, что:

$$-\!1 \leq \frac{x}{2} \leq 1 \implies -2 \leq x \leq 2.$$

Шаг 3. Таблица значений

Дана таблица:

$$\begin{array}{|c|c|c|} \hline x & 0 & -\frac{5\pi}{4} \\ \hline y = \frac{x}{2} & 0 & -2 \\ \hline y = \sin x & 0 & \sin\left(-\frac{5\pi}{4}\right) = -\frac{\sqrt{2}}{2} \approx -0.7 \\ \hline \end{array}$$

Обратим внимание: в точке $x = -\frac{5\pi}{4} \approx -3.93$ значение $y = \frac{x}{2} = -1.965$ (в таблице округлено до -2). Значение $\sin x \approx -0.7$, следовательно, в этой точке не равенство, но может быть пересечение близко к ней.

Шаг 4. Графический анализ

Построим графики:

• $y = \sin x$ — колебательная кривая.
• $y = \frac{x}{2}$ — прямая.

Из графика видно, что уравнение имеет три решения:

• Одно решение в точке $x=0$ (тривиальное).
• Второе решение находится в отрицательной области ближе к $-2$.
• Третье решение находится в положительной области около $1.5$.

Итог:

$$\boxed{ \text{Уравнение } \sin x = \frac{x}{2} \text{ имеет } 3 \text{ решения.} }$$