ГДЗ по Алгебре 10-11 Класс Номер 739 Алимов — Подробные Ответы

Найти все корни уравнения, принадлежащие отрезку [0; 3пи]:

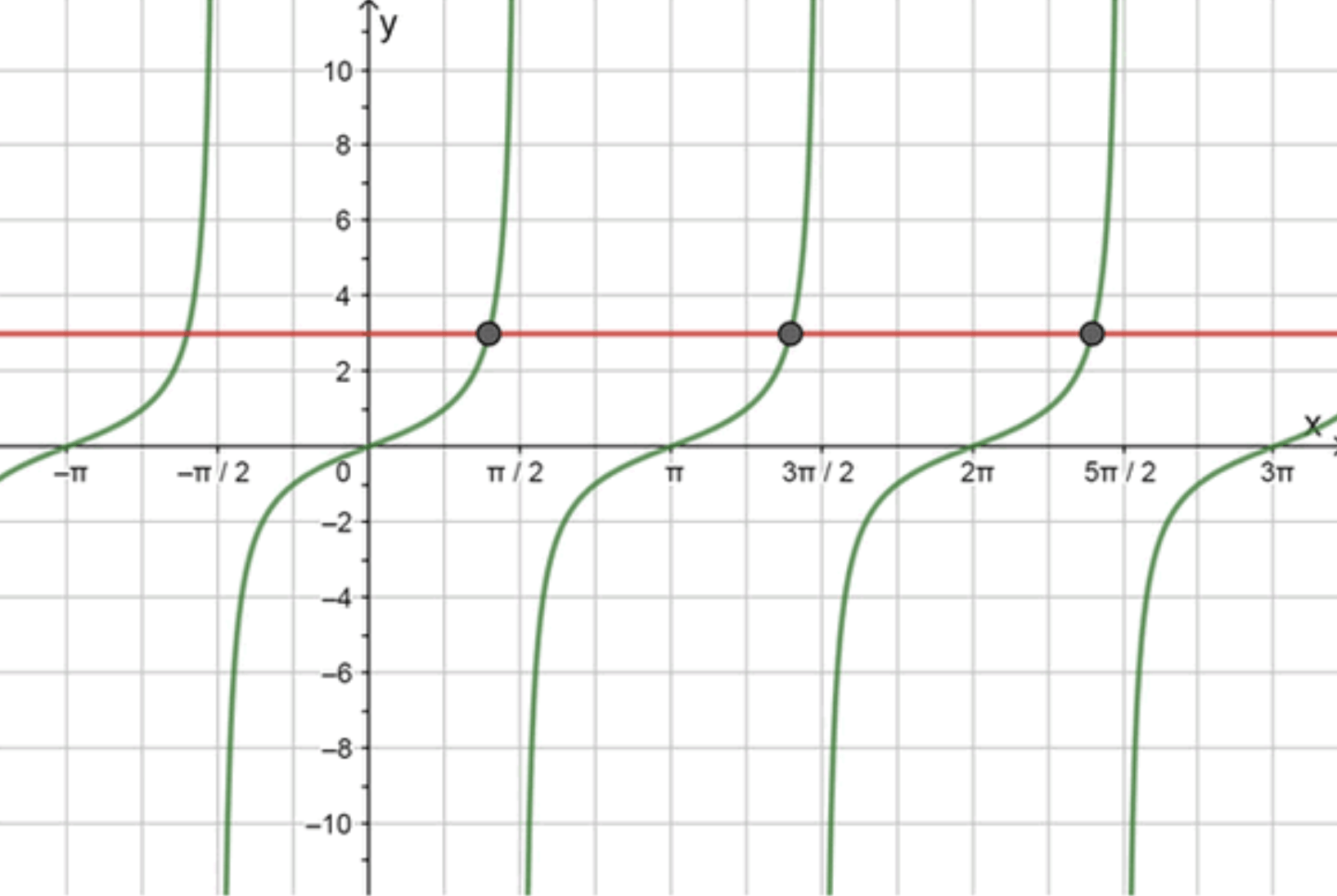
1. tg х = 3;
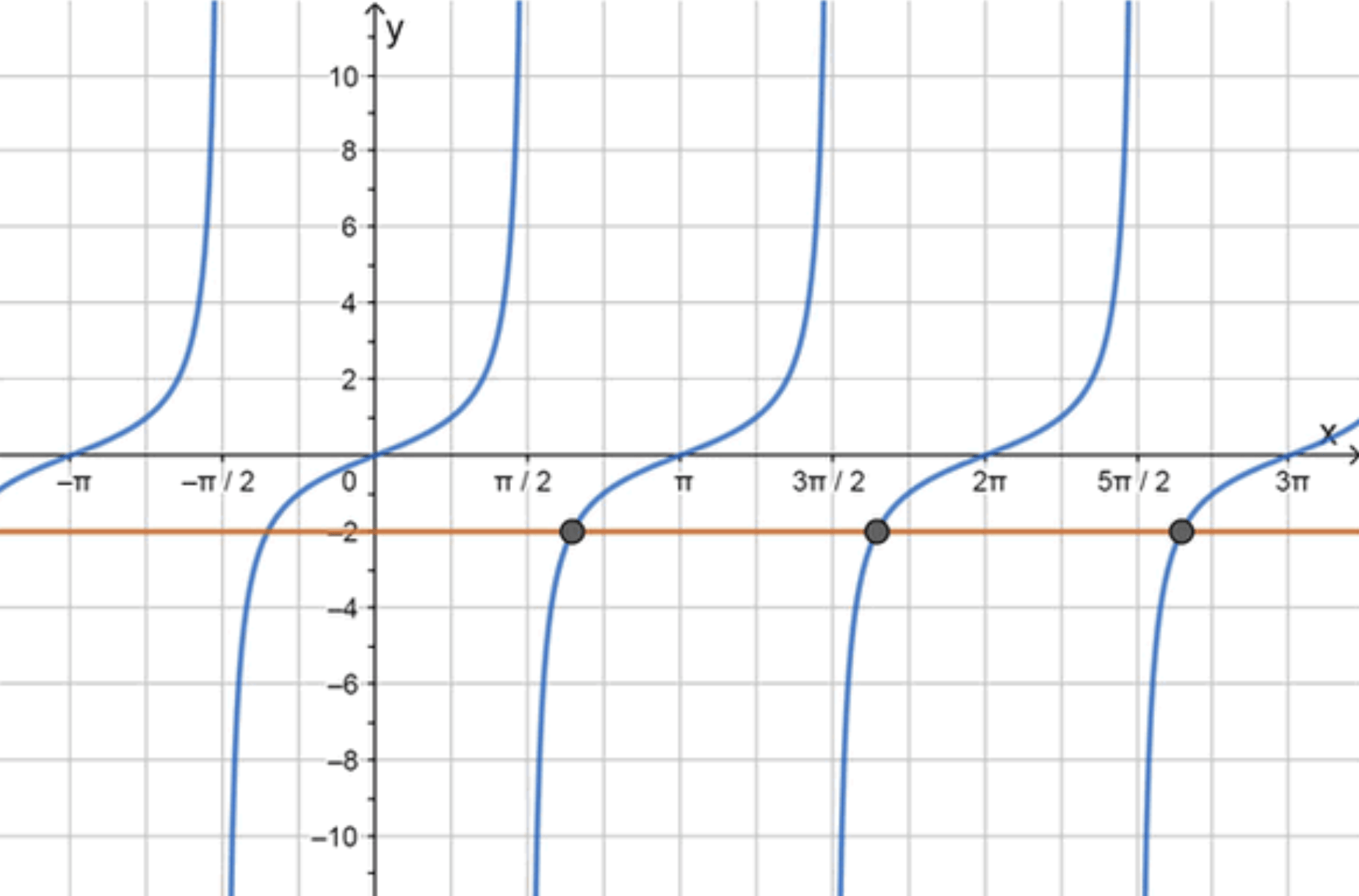
2. tg х = -2.

Требуется найти корни уравнения на отрезке $[0; 3\pi]$:

$\operatorname{tg} x = 3$;
$x = \operatorname{arctg} 3 + \pi n$;

График функции:

Значения на искомом отрезке:
$x_1 = \operatorname{arctg} 3$;
$x_2 = \operatorname{arctg} 3 + \pi$;
$x_3 = \operatorname{arctg} 3 + 2\pi$;

$\operatorname{tg} x = -2$;
$x = -\operatorname{arctg} 2 + \pi n$;

График функции:

Значения на искомом отрезке:
$x_1 = -\operatorname{arctg} 2 + \pi$;
$x_2 = -\operatorname{arctg} 2 + 2\pi$;
$x_3 = -\operatorname{arctg} 2 + 3\pi$

Найти все корни уравнения

$$\tg x = a$$

на отрезке

$$[0; 3\pi]$$

для следующих значений $a$:

1. $a = 3$
2. $a = -2$

Важные сведения

• Функция тангенса $\tg x$ — периодическая с периодом $\pi$:

$$\tg (x + \pi) = \tg x$$

• Область определения:

$$x \neq \frac{\pi}{2} + \pi n, \quad n \in \mathbb{Z}$$

(в этих точках вертикальные асимптоты, тангенс не определён).

• Общее решение уравнения:

$$\tg x = a \quad \Rightarrow \quad x = \arctg a + \pi n, \quad n \in \mathbb{Z}$$

где $\arctg a$ — главный корень, лежащий в интервале $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$.

1) Уравнение

$$\tg x = 3$$

Шаг 1: Найдём главный корень

$$x_0 = \arctg 3$$

Это угол, тангенс которого равен 3. Значение приблизительно:

$$\arctg 3 \approx 1.249 \text{ (радиан)}$$

Шаг 2: Запишем общее решение

$$x = \arctg 3 + \pi n, \quad n \in \mathbb{Z}$$

Шаг 3: Найдём все $n$, для которых корни лежат на отрезке $[0; 3\pi]$

Поскольку $\pi \approx 3.1416$, то

$$0 \leq \arctg 3 + \pi n \leq 3\pi$$

Подставим:

$$0 \leq 1.249 + 3.1416 n \leq 9.4248$$

Левая граница:

$$1.249 + 3.1416 n \geq 0 \implies 3.1416 n \geq -1.249 \implies n \geq -0.397$$

Правая граница:

$$1.249 + 3.1416 n \leq 9.4248 \implies 3.1416 n \leq 8.1758 \implies n \leq 2.603$$

Итог: целые $n$, удовлетворяющие неравенствам:

$$n = 0, 1, 2$$

Шаг 4: Найдём корни на отрезке

• Для $n=0$:

$$x_1 = \arctg 3 \approx 1.249$$

• Для $n=1$:

$$x_2 = \arctg 3 + \pi \approx 1.249 + 3.1416 = 4.3906$$

• Для $n=2$:

$$x_3 = \arctg 3 + 2\pi \approx 1.249 + 6.2832 = 7.5322$$

Все три значения лежат в $[0; 3\pi]$, поскольку $3\pi \approx 9.4248$.

2) Уравнение

$$\tg x = -2$$

Шаг 1: Найдём главный корень

$$x_0 = \arctg (-2) = — \arctg 2$$

Поскольку $\arctg 2 \approx 1.107$,

$$x_0 \approx -1.107$$

Шаг 2: Запишем общее решение

$$x = -\arctg 2 + \pi n, \quad n \in \mathbb{Z}$$

Шаг 3: Найдём $n$, для которых корни лежат на отрезке $[0; 3\pi]$

$$0 \leq -1.107 + 3.1416 n \leq 9.4248$$

Левая граница:

$$-1.107 + 3.1416 n \geq 0 \implies 3.1416 n \geq 1.107 \implies n \geq 0.352$$

Правая граница:

$$-1.107 + 3.1416 n \leq 9.4248 \implies 3.1416 n \leq 10.5318 \implies n \leq 3.354$$

Итог: целые $n$:

$$n = 1, 2, 3$$

Шаг 4: Найдём корни на отрезке

• Для $n=1$:

$$x_1 = -1.107 + 3.1416 \approx 2.0346$$

• Для $n=2$:

$$x_2 = -1.107 + 6.2832 \approx 5.1762$$

• Для $n=3$:

$$x_3 = -1.107 + 9.4248 \approx 8.318$$

Все три значения лежат в $[0; 3\pi]$.