ГДЗ по Алгебре 10-11 Класс Номер 733 Алимов — Подробные Ответы

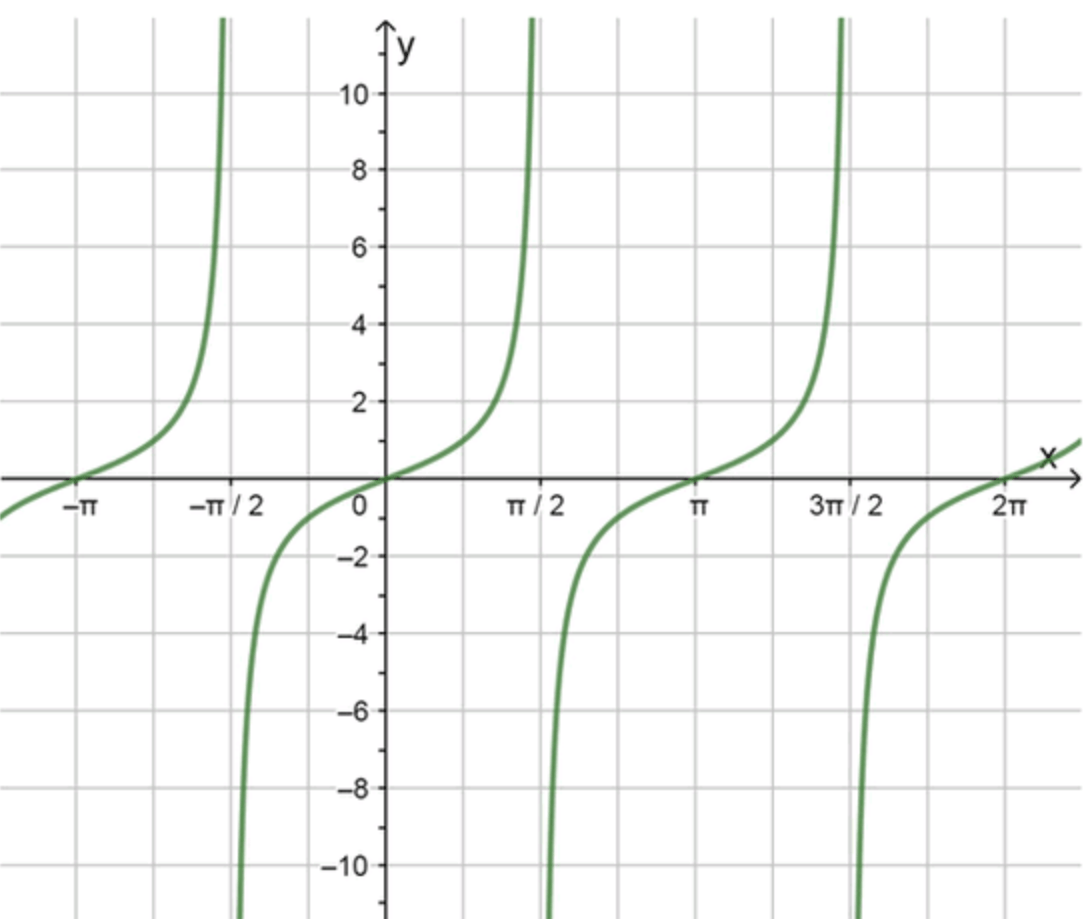
(Устно.) Выяснить, при каких значениях х из промежутка [-пи; 2пи] функция у — tg х принимает:

1. значение, равное 0;
2. положительные значения;
3. отрицательные значения.

Воспользуемся графиком функции $y = \operatorname{tg} x$ на отрезке $[-π; 2π]$:

1. Функция принимает значение, равное:
   $y = 0, \text{ при } x = -π, 0, π, 2π;$
2. Функция принимает положительные значения при:
   $-π < x < -\frac{π}{2};$
   $0 < x < \frac{π}{2};$
   $π < x < \frac{3π}{2};$
3. Функция принимает отрицательные значения при:
   $-\frac{π}{2} \leqslant x \leqslant 0;$
   $\frac{π}{2} < x < π;$
   $\frac{3π}{2} < x < 2π;$

Задание:

Использовать график функции $y = \tan x$ на отрезке $[-π; 2π]$ и определить:

1. При каких значениях $x$ функция принимает значение $y = 0$.
2. При каких промежутках $x$ функция принимает положительные значения.
3. При каких промежутках $x$ функция принимает отрицательные значения.

Теоретическая база:

Функция $y = \tan x$ (тангенс угла $x$) — это периодическая функция с периодом $\pi$, определённая как отношение:

$$\tan x = \frac{\sin x}{\cos x}$$

где $\sin x$ и $\cos x$ — синус и косинус угла $x$.

Особенности функции тангенс:

• Тангенс не определён в точках, где $\cos x = 0$, т.е. в точках:

$$x = \pm \frac{\pi}{2}, \pm \frac{3\pi}{2}, \ldots$$

В этих точках функция имеет вертикальные асимптоты.

• Функция периодична с периодом $\pi$, то есть:

$$\tan(x + \pi) = \tan x$$

• Функция принимает значение 0 в тех точках, где $\sin x = 0$, а $\cos x \neq 0$, то есть:

$$x = k\pi, \quad k \in \mathbb{Z}$$

1) При каких значениях $x$ функция $y = \tan x$ равна нулю?

$$\tan x = 0 \quad \Leftrightarrow \quad \sin x = 0 \quad \text{и} \quad \cos x \neq 0$$

Синус равен нулю в точках:

$$x = k\pi, \quad k \in \mathbb{Z}$$

На отрезке $[-π; 2π]$ это точки:

$$x = -\pi, 0, \pi, 2\pi$$

В этих точках тангенс пересекает ось $OX$ и принимает значение $y=0$.

2) При каких промежутках $x$ функция $y = \tan x$ положительна?

Для изучения знака функции нужно рассмотреть знаки числителя и знаменателя $\frac{\sin x}{\cos x}$.

• Тангенс положителен, когда $\sin x$ и $\cos x$ имеют одинаковый знак (оба положительные или оба отрицательные).

На интервале $[-π; 2π]$ рассмотрим части:

• Интервал $-\pi < x < -\frac{\pi}{2}$:
  • $\sin x$ в этом промежутке отрицателен (т.к. синус отрицателен на третьей четверти круга).
  • $\cos x$ в этом же промежутке отрицателен (т.к. косинус отрицателен на второй половине от $\pi$ до $-\pi$).
  • Оба отрицательны $\Rightarrow$ $\tan x > 0$.
• Интервал $0 < x < \frac{\pi}{2}$:
  • $\sin x > 0$
  • $\cos x > 0$
  • Оба положительны $\Rightarrow$ $\tan x > 0$.
• Интервал $\pi < x < \frac{3\pi}{2}$:
  • $\sin x < 0$ (третья четверть круга)
  • $\cos x < 0$
  • Оба отрицательны $\Rightarrow$ $\tan x > 0$.

3) При каких промежутках $x$ функция $y = \tan x$ отрицательна?

• Тангенс отрицателен, когда $\sin x$ и $\cos x$ имеют противоположные знаки.

Рассмотрим интервалы:

• Интервал $-\frac{\pi}{2} \leq x \leq 0$:
  • $\sin x \leq 0$
  • $\cos x > 0$ (т.к. косинус положителен на 1-ой четверти и около 0)
  • Знаки разные $\Rightarrow \tan x < 0$.
• Интервал $\frac{\pi}{2} < x < \pi$:
  • $\sin x > 0$
  • $\cos x < 0$
  • Знаки разные $\Rightarrow \tan x < 0$.
• Интервал $\frac{3\pi}{2} < x < 2\pi$:
  • $\sin x > 0$
  • $\cos x < 0$
  • Знаки разные $\Rightarrow \tan x < 0$.

Итог:

• $y = 0$ при $x = -\pi, 0, \pi, 2\pi$.
• $y > 0$ на интервалах:

  $$-\pi < x < -\frac{\pi}{2}; \quad 0 < x < \frac{\pi}{2}; \quad \pi < x < \frac{3\pi}{2};$$

• $y < 0$ на интервалах:

  $$-\frac{\pi}{2} \leq x \leq 0; \quad \frac{\pi}{2} < x < \pi; \quad \frac{3\pi}{2} < x < 2\pi;$$