
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 731 Алимов — Подробные Ответы
Построить график функции:
- y = sin|x|;
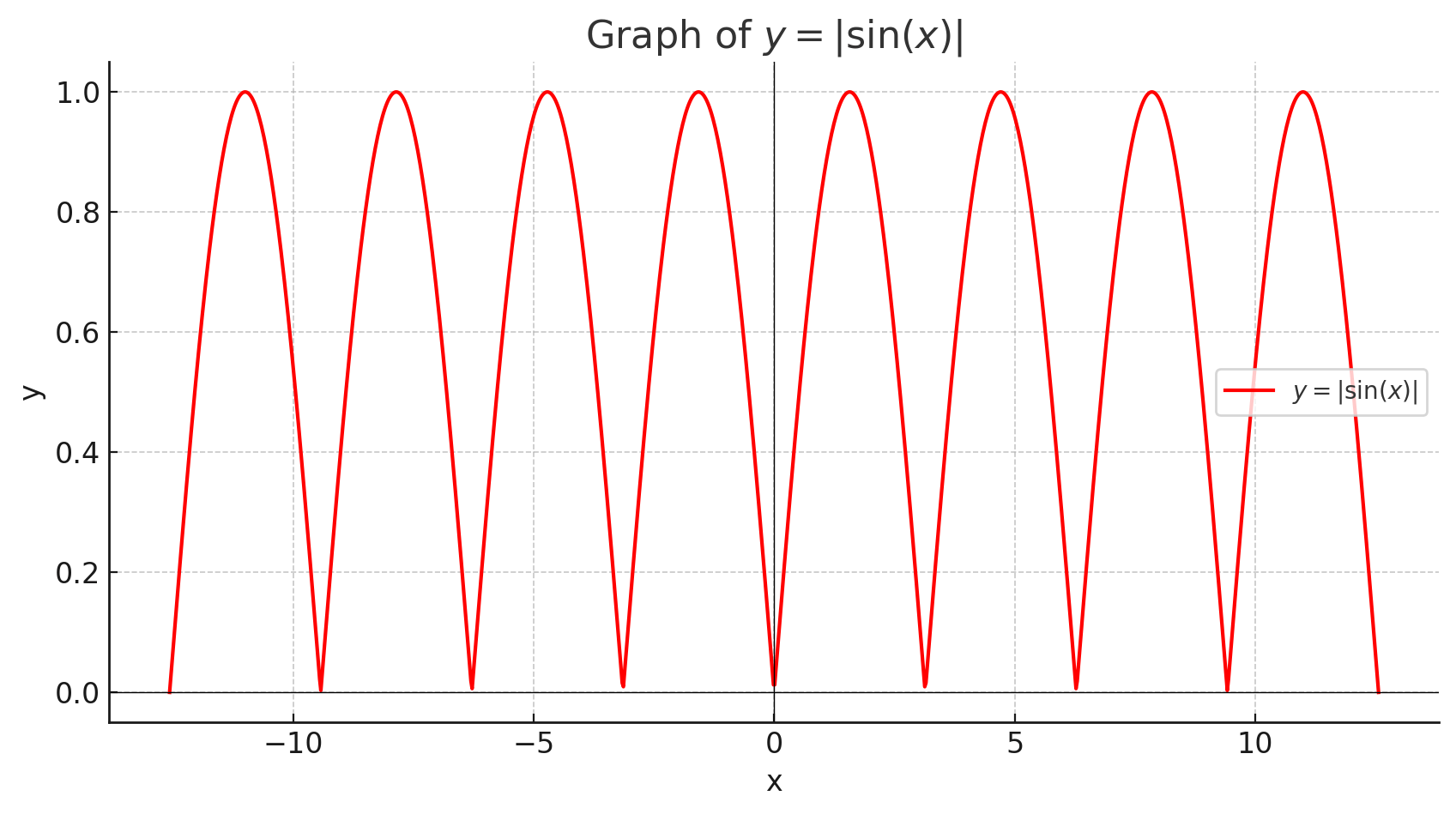
- y = |sinx|.
1)
а) Область определения:
б) Область значений:
в) Период функции:
г) Функция четная:
д) Нули функции:
е) Максимальные значения:
ж) Минимальные значения:
2)
а) Область определения:
б) Область значений:
в) Период функции:
г) Функция четная:
д) Нули функции:
е) Максимальные значения:
ж) Минимальные значения:
1) Функция
а) Область определения функции
Область определения — это множество всех значений , при которых функция определена.
Функция состоит из двух операций:
- Берём модуль , который определён для всех (все вещественные числа),
- Берём синус от результата — синус определён для всех вещественных чисел.
Следовательно,
б) Область значений функции
Область значений — это множество всех значений , которые может принимать функция.
- Синус принимает значения на промежутке от -1 до 1:
- Модуль всегда неотрицателен, но внутри синуса это не меняет амплитуды:
- Значит, область значений функции — от -1 до 1:
в) Период функции
Функция периодическая, если существует число , для которого
Для :
Чтобы период сохранялся для модуля аргумента, должно вести себя так, чтобы синус оставался тем же.
Период синуса , поэтому:
г) Чётность функции
Функция называется чётной, если
Проверим:
Значит, функция чётная.
д) Нули функции
Нули — значения , при которых .
Решаем уравнение:
Значения синуса равные нулю:
Заменяем :
Отсюда:
е) Максимальные значения
Максимальное значение синуса — 1:
Решаем:
Тогда:
ж) Минимальные значения
Минимальное значение синуса — -1:
Решаем:
Но поскольку , отрицательное значение внутри модуля невозможно, значит нужно уточнить:
- ,
- .
Однако, не может быть отрицательным, значит решения с возможны только при .
Итог:
2) Функция
а) Область определения функции
- Синус определён для всех вещественных чисел,
- Модуль синуса — тоже для всех чисел.
Следовательно:
б) Область значений функции
- Синус принимает значения от -1 до 1,
- Модуль всегда неотрицателен, поэтому:
и
в) Период функции
Период функции — наименьшее , для которого
Рассмотрим случаи:
Из первого:
Из второго:
Наименьший период — .
г) Чётность функции
Проверим:
Функция чётная.
д) Нули функции
Решаем уравнение:
Корни:
е) Максимальные значения
Максимум достигается при:
Корни:
Объединённо:
ж) Минимальные значения
Минимум достигается в нулях синуса:


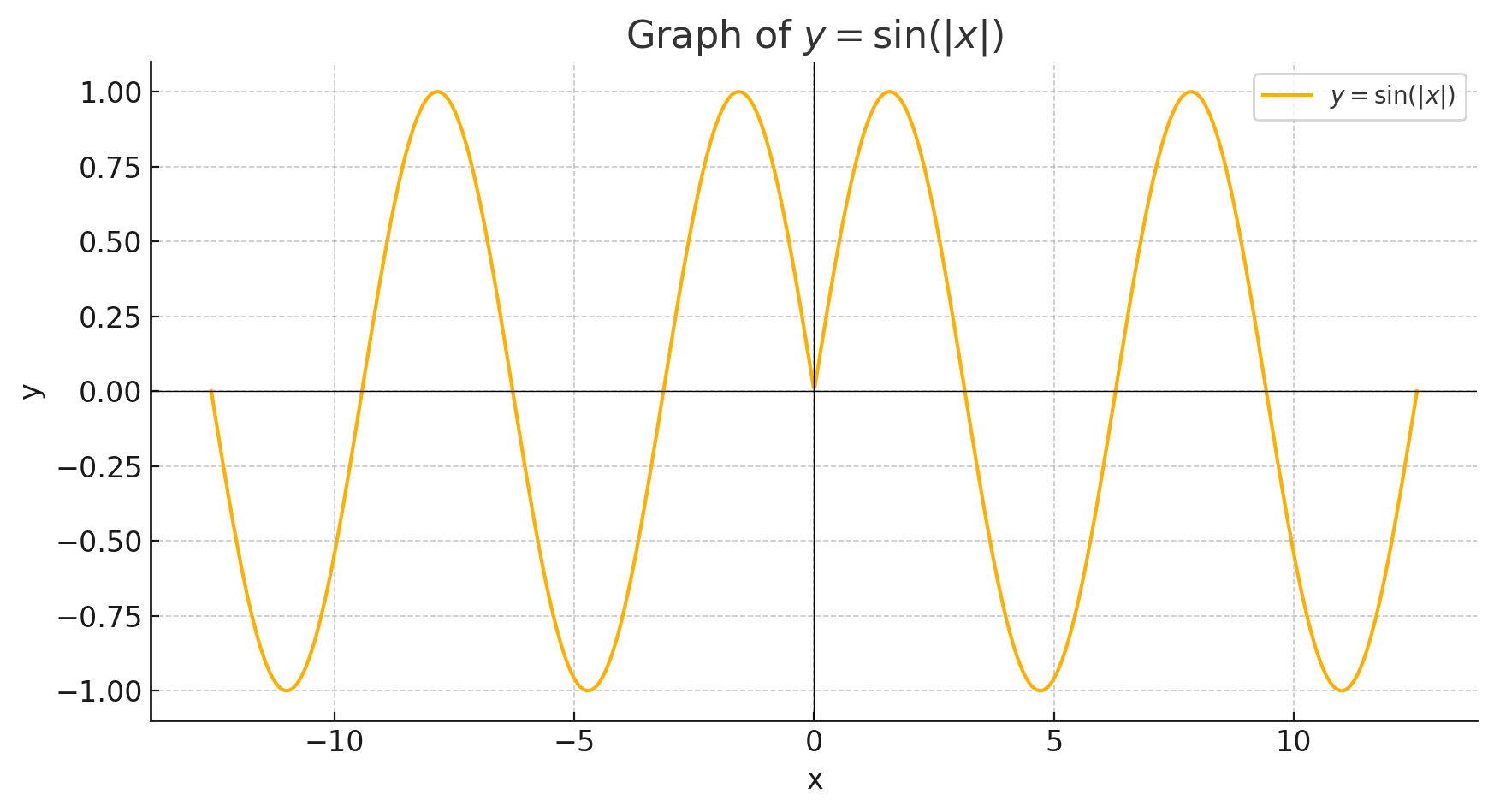

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!