ГДЗ по Алгебре 10-11 Класс Номер 722 Алимов — Подробные Ответы

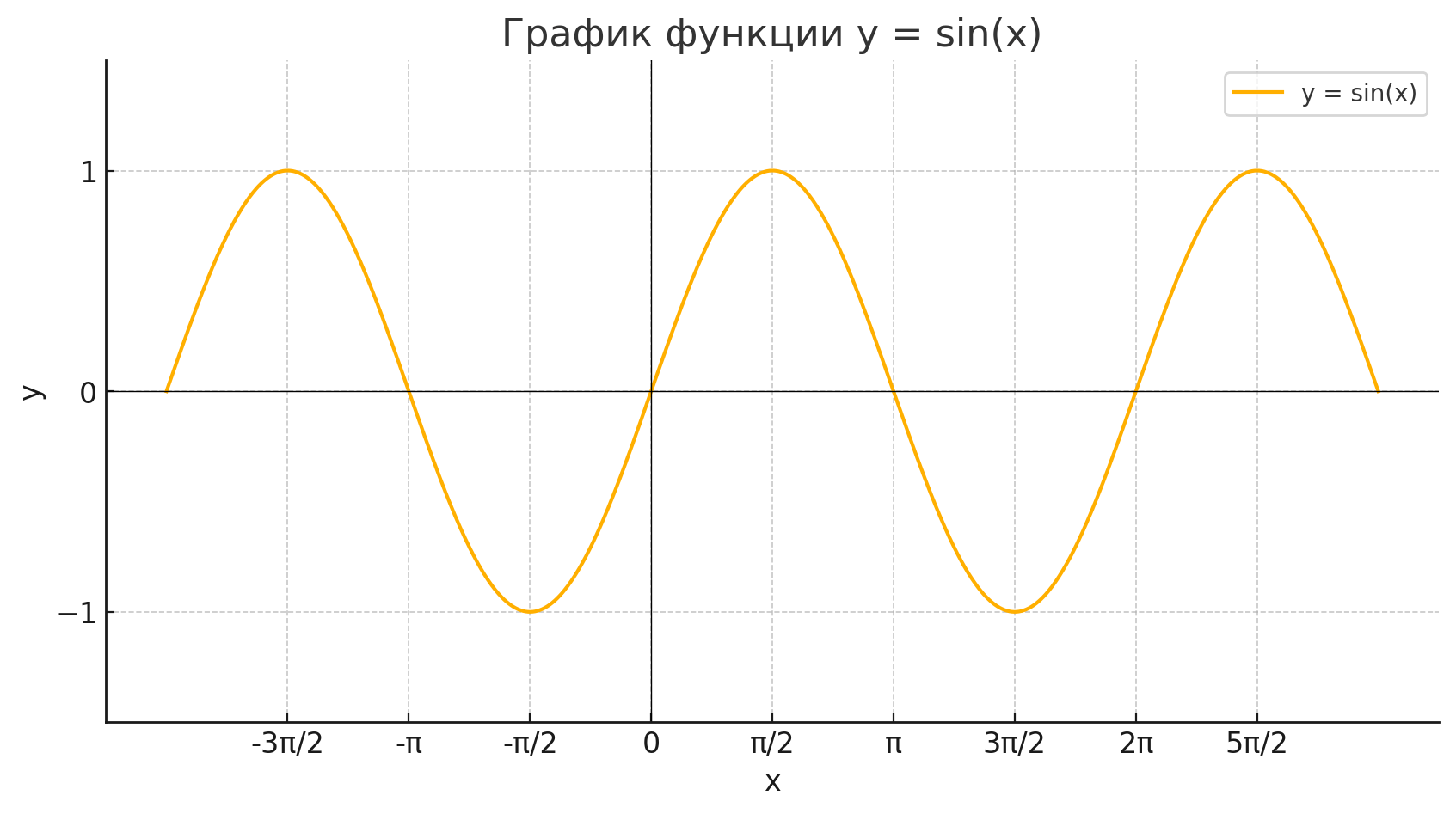
Разбить данный отрезок на два отрезка так, чтобы на одном из них функция у = sin х возрастала, а на другом убывала:

1. [0;пи];
2. [пи/2; 2пи];
3. [-пи; 0];
4. [-2пи;-пи].

Воспользуемся графиком функции $y = \sin x$:

1. $[0; \pi]$;
   Возрастает на отрезке $\left[ 0 ; \frac{\pi}{2} \right]$;
   Убывает на отрезке $\left[ \frac{\pi}{2} ; \pi \right]$;
2. $\left[ \frac{\pi}{2} ; 2\pi \right]$;
   Возрастает на отрезке $\left[ \frac{3\pi}{2} ; 2\pi \right]$;
   Убывает на отрезке $\left[ \frac{\pi}{2} ; \frac{3\pi}{2} \right]$;
3. $[-π; 0]$;
   Возрастает на отрезке $\left[ -\frac{\pi}{2} ; 0 \right]$;
   Убывает на отрезке $\left[ -\pi ; -\frac{\pi}{2} \right]$;
4. $[-2π; -π]$;
   Возрастает на отрезке $\left[ -2\pi ; -\frac{3\pi}{2} \right]$;
   Убывает на отрезке $\left[ -\frac{3\pi}{2} ; -\pi \right]$

Воспользуемся графиком функции $y = \sin x$ и исследуем её поведение на нескольких отрезках.

Дано:

Функция $y = \sin x$.

Необходимо определить, на каких отрезках функция возрастает, а на каких — убывает, в частности на указанных интервалах.

Шаг 1. Общие сведения о функции $y = \sin x$:

• Функция $\sin x$ — периодическая с периодом $2\pi$.
• Значения функции колеблются от -1 до 1.
• Основные точки, где функция меняет направление (возрастает/убывает):
  • Максимумы в точках $x = \frac{\pi}{2} + 2k\pi$, где $k \in \mathbb{Z}$, значение функции $y = 1$.
  • Минимумы в точках $x = \frac{3\pi}{2} + 2k\pi$, где $k \in \mathbb{Z}$, значение функции $y = -1$.
  • Нули в точках $x = k\pi$, где $k \in \mathbb{Z}$, значение функции $y = 0$.

Шаг 2. Исследование функции на производную

Для определения возрастания или убывания функции используем её производную:

$$y = \sin x \implies y’ = \cos x$$

• Если $y’ > 0$ на некотором промежутке — функция возрастает на этом промежутке.
• Если $y’ < 0$ на некотором промежутке — функция убывает на этом промежутке.

Шаг 3. Анализ поведения функции на каждом указанном отрезке

1) Отрезок $[0; \pi]$:

• Производная: $y’ = \cos x$.
• Значения косинуса на $[0; \pi]$:
  • На $\left[0; \frac{\pi}{2}\right]$, $\cos x > 0$ (косинус убывает от 1 до 0).
  • На $\left[\frac{\pi}{2}; \pi\right]$, $\cos x < 0$ (косинус убывает от 0 до -1).

Вывод:

• Функция возрастает на отрезке $\left[0; \frac{\pi}{2}\right]$, так как $y’ > 0$.
• Функция убывает на отрезке $\left[\frac{\pi}{2}; \pi\right]$, так как $y’ < 0$.

2) Отрезок $\left[\frac{\pi}{2}; 2\pi\right]$:

• Анализируем производную на двух промежутках:
  • $\left[\frac{\pi}{2}; \frac{3\pi}{2}\right]$, где $\cos x < 0$ — функция убывает.
  • $\left[\frac{3\pi}{2}; 2\pi\right]$, где $\cos x > 0$ — функция возрастает.

Вывод:

• Функция убывает на $\left[\frac{\pi}{2}; \frac{3\pi}{2}\right]$.
• Функция возрастает на $\left[\frac{3\pi}{2}; 2\pi\right]$.

3) Отрезок $[- \pi; 0]$:

• Производная $y’ = \cos x$ на этом промежутке:
  • $\left[-\pi; -\frac{\pi}{2}\right]$, $\cos x < 0$ — функция убывает.
  • $\left[-\frac{\pi}{2}; 0\right]$, $\cos x > 0$ — функция возрастает.

Вывод:

• Функция убывает на $\left[-\pi; -\frac{\pi}{2}\right]$.
• Функция возрастает на $\left[-\frac{\pi}{2}; 0\right]$.

4) Отрезок $[-2\pi; -\pi]$:

• Аналогично, разбиваем на два промежутка:
  • $\left[-2\pi; -\frac{3\pi}{2}\right]$, $\cos x > 0$ — функция возрастает.
  • $\left[-\frac{3\pi}{2}; -\pi\right]$, $\cos x < 0$ — функция убывает.

Вывод:

• Функция возрастает на $\left[-2\pi; -\frac{3\pi}{2}\right]$.
• Функция убывает на $\left[-\frac{3\pi}{2}; -\pi\right]$.

Итог:

Дополнительные пояснения:

• Точки $x = k \pi$ (где $k \in \mathbb{Z}$) — это нули функции, там $\sin x = 0$.
• Точки $x = \frac{\pi}{2} + 2k\pi$ — максимумы (локальные), где функция меняет рост на убывание.
• Точки $x = \frac{3\pi}{2} + 2k\pi$ — минимумы (локальные), где функция меняет убывание на рост.
• Производная $\cos x$ — меняет знак именно в этих точках, что и объясняет поведение функции.