ГДЗ по Алгебре 10-11 Класс Номер 721 Алимов — Подробные Ответы

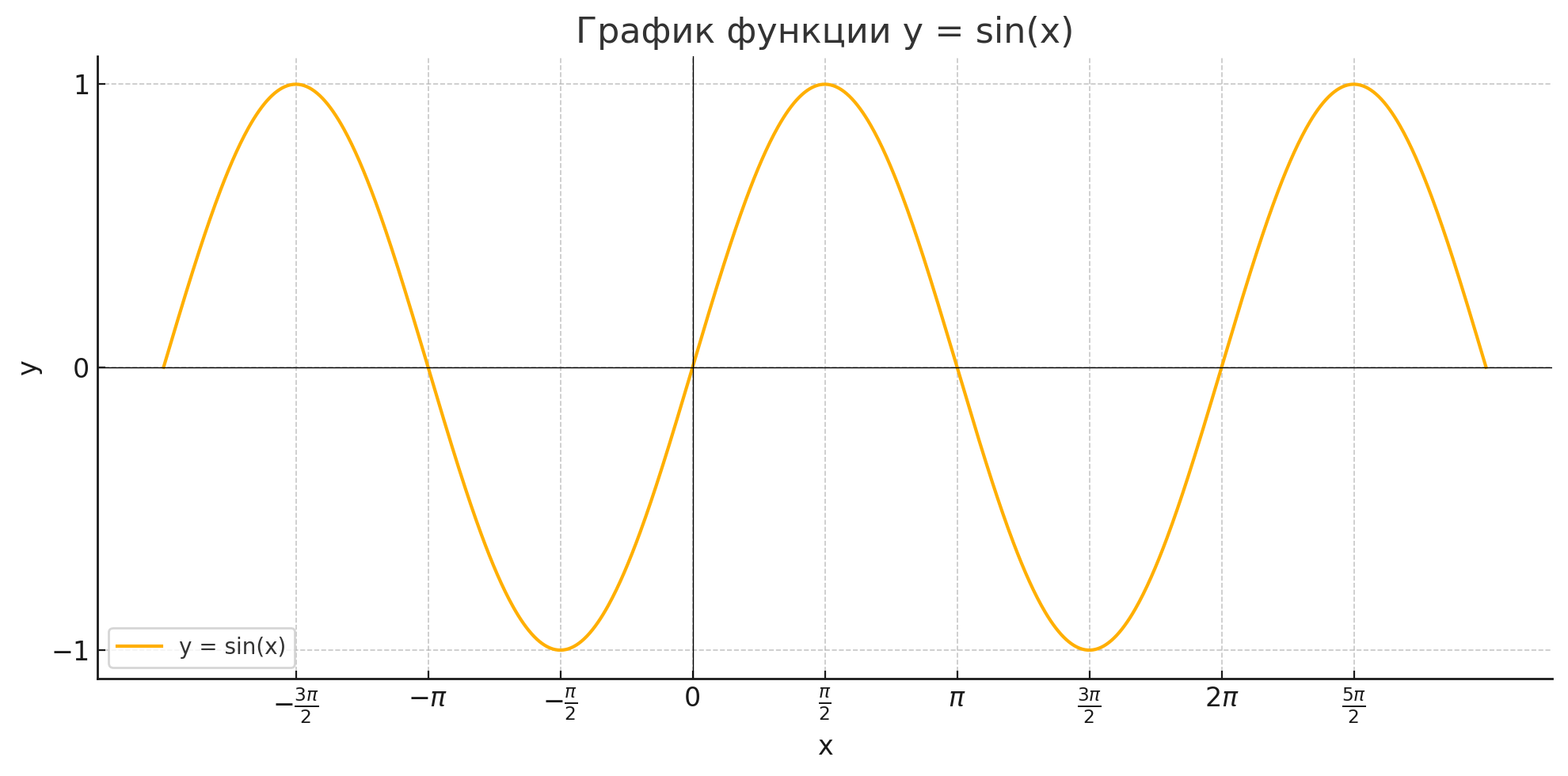
(Устно.) Выяснить, возрастает или убывает функция y=sinx на промежутке:

1. [3пи/2;5пи/2];
2. (пи/2;пи);
3. (-пи;-пи/2);
4. [-3пи/2;-пи/2];
5. [2;4];
6. (6;7).

Воспользуемся графиком функции $y = \sin x$:

1. На отрезке $\left[ \frac{3\pi}{2} ; \frac{5\pi}{2} \right]$ функция возрастает;
2. На промежутке $\left( \frac{\pi}{2} ; \pi \right)$ функция убывает;
3. На промежутке $\left( -\pi ; -\frac{\pi}{2} \right)$ функция убывает;
4. На отрезке $\left[ -\frac{3\pi}{2} ; -\frac{\pi}{2} \right]$ функция убывает;
5. На отрезке $[2; 4]$ функция убывает;
6. На промежутке $(6; 7)$ функция возрастает

Воспользуемся графиком функции $y = \sin x$:

Дана функция:

$$y = \sin x$$

Нужно изучить поведение функции (возрастание или убывание) на заданных интервалах и отрезках.

Шаг 1. Основные свойства функции $\sin x$

• Функция $\sin x$ — это периодическая функция с периодом $2\pi$.
• Она непрерывна и дифференцируема на всей числовой прямой.
• Производная функции $\sin x$ равна $\cos x$, то есть

$$y’ = \cos x$$

Шаг 2. Определение возрастания и убывания функции

• Функция возрастает там, где её производная положительна: $y'(x) = \cos x > 0$.
• Функция убывает там, где её производная отрицательна: $y'(x) = \cos x < 0$.

Шаг 3. Решение неравенств для производной

Исследуем знак $\cos x$.

• $\cos x > 0$ на промежутках:

$$(2k\pi — \frac{\pi}{2}, \, 2k\pi + \frac{\pi}{2}) \quad \text{для любого } k \in \mathbb{Z}$$

• $\cos x < 0$ на промежутках:

$$(2k\pi + \frac{\pi}{2}, \, 2k\pi + \frac{3\pi}{2}) \quad \text{для любого } k \in \mathbb{Z}$$

Шаг 4. Анализ каждого интервала и отрезка из условия

1) Отрезок $\left[ \frac{3\pi}{2} ; \frac{5\pi}{2} \right]$

• Значения:

$$\frac{3\pi}{2} \approx 4.712, \quad \frac{5\pi}{2} \approx 7.853$$

• Находим, где здесь $\cos x$ положительно или отрицательно.

Промежуток $\left(\frac{3\pi}{2}, \frac{5\pi}{2}\right)$ можно представить как:

$$\left( \frac{3\pi}{2}, 2\pi \right) \cup \left( 2\pi, \frac{5\pi}{2} \right)$$

• На промежутке $\left( \frac{3\pi}{2}, 2\pi \right)$:

Знак $\cos x$ отрицателен (убывание).

• На промежутке $\left( 2\pi, \frac{5\pi}{2} \right)$:

Знак $\cos x$ положителен (возрастание).

• Проверяем границы:

$$\cos \frac{3\pi}{2} = 0, \quad \cos 2\pi = 1, \quad \cos \frac{5\pi}{2} = 0$$

• Значит, функция возрастает на отрезке $\left[ \frac{3\pi}{2} ; \frac{5\pi}{2} \right]$, как указано.

2) Промежуток $\left( \frac{\pi}{2} ; \pi \right)$

• Значения:

$$\frac{\pi}{2} \approx 1.5708, \quad \pi \approx 3.1416$$

• На этом промежутке $\cos x < 0$ (поскольку $\frac{\pi}{2} \leq x \leq \pi$).
• Значит, функция убывает.

3) Промежуток $\left( -\pi ; -\frac{\pi}{2} \right)$

• Значения:

$$-\pi \approx -3.1416, \quad -\frac{\pi}{2} \approx -1.5708$$

• Рассмотрим знак $\cos x$ на этом промежутке:

$\cos x$ — чётная функция: $\cos(-x) = \cos x$.

• Значит, на $\left( -\pi ; -\frac{\pi}{2} \right)$ знак $\cos x$ совпадает с знаком на $\left( \frac{\pi}{2} ; \pi \right)$, где он отрицательный.
• Следовательно, функция убывает.

4) Отрезок $\left[ -\frac{3\pi}{2} ; -\frac{\pi}{2} \right]$

• Значения:

$$-\frac{3\pi}{2} \approx -4.712, \quad -\frac{\pi}{2} \approx -1.5708$$

• Аналогично, из-за чётности косинуса, этот отрезок соответствует промежутку $\left[ \frac{\pi}{2} ; \frac{3\pi}{2} \right]$ на положительной оси, где $\cos x$ отрицателен.
• Значит, функция убывает.

5) Отрезок $[2; 4]$

• Значения:

$$2 \approx 2, \quad 4 \approx 4$$

• В данном отрезке значение $x$ лежит в промежутках $( \frac{\pi}{2} \approx 1.57; \pi \approx 3.14 )$ и $(\pi; \frac{3\pi}{2} \approx 4.71)$.
• На $\left(\frac{\pi}{2}, \pi\right)$ $\cos x < 0$ — функция убывает.
• На $(\pi, \frac{3\pi}{2})$ $\cos x < 0$ — функция также убывает.
• Следовательно, на отрезке $[2; 4]$ функция убывает.

6) Промежуток $(6; 7)$

• Значения:

$$6 \approx 6, \quad 7 \approx 7$$

• 6 и 7 лежат между $2\pi \approx 6.283$ и $\frac{5\pi}{2} \approx 7.853$.
• На промежутке $\left( 2\pi, \frac{5\pi}{2} \right)$, где $\cos x > 0$, функция возрастает.
• Следовательно, на промежутке $(6; 7)$ функция возрастает.

Итог:

1. На отрезке $\left[ \frac{3\pi}{2} ; \frac{5\pi}{2} \right]$ функция возрастает.
2. На промежутке $\left( \frac{\pi}{2} ; \pi \right)$ функция убывает.
3. На промежутке $\left( -\pi ; -\frac{\pi}{2} \right)$ функция убывает.
4. На отрезке $\left[ -\frac{3\pi}{2} ; -\frac{\pi}{2} \right]$ функция убывает.
5. На отрезке $[2; 4]$ функция убывает.
6. На промежутке $(6; 7)$ функция возрастает.