ГДЗ по Алгебре 10-11 Класс Номер 710 Алимов — Подробные Ответы

Разбить данный отрезок на два отрезка так, чтобы на одном из них функция у = cos х возрастала, а на другом убывала:

1. [пи/2; 3пи/2];
2. [- пи/2; пи/2];
3. [0; 3пи/2];
4. [-пи; пи/2]

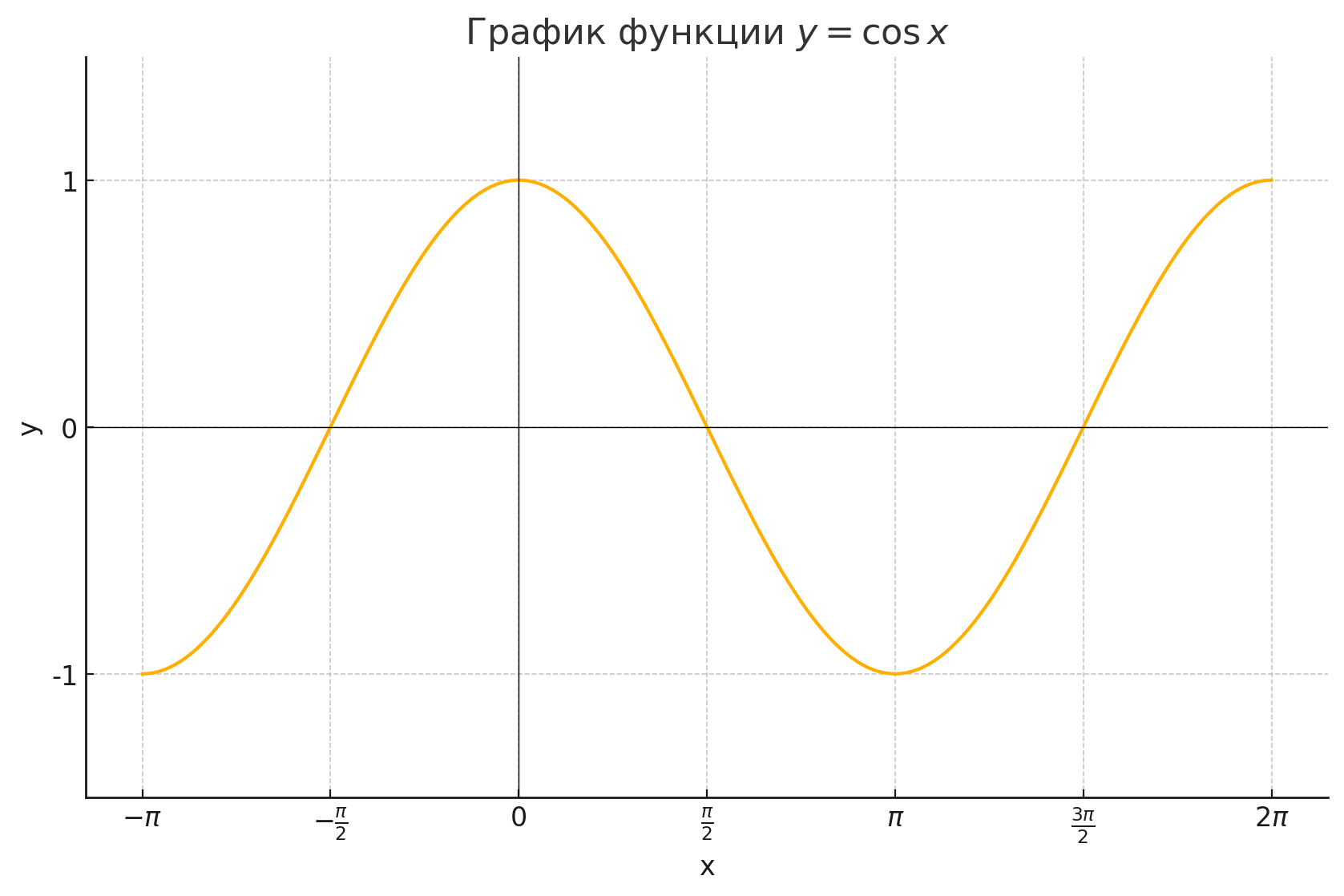
Воспользуемся графиком функции $y = \cos x$:

1. $\left[ \frac{\pi}{2}; \frac{3\pi}{2} \right]$;
   Возрастает на отрезке $\left[ \pi; \frac{3\pi}{2} \right]$;
   Убывает на отрезке $\left[ \frac{\pi}{2}; \pi \right]$;
2. $\left[ -\frac{\pi}{2}; \frac{\pi}{2} \right]$;
   Возрастает на отрезке $\left[ -\frac{\pi}{2}; 0 \right]$;
   Убывает на отрезке $\left[ 0; \frac{\pi}{2} \right]$;
3. $\left[ 0; \frac{3\pi}{2} \right]$;
   Возрастает на отрезке $\left[ \pi; \frac{3\pi}{2} \right]$;
   Убывает на отрезке $[0; \pi]$;
4. $\left[ -\pi; \frac{\pi}{2} \right]$;
   Возрастает на отрезке $[-π; 0]$;
   Убывает на отрезке $\left[ 0; \frac{\pi}{2} \right]$

Дано:

Функция:

$$y = \cos x$$

График функции — периодическая волна с периодом $2\pi$, колеблющаяся между 1 и -1.

Основные свойства функции $y = \cos x$:

• Период $T = 2\pi$.
• Максимум $y = 1$ достигается в точках $x = 2k\pi$, где $k \in \mathbb{Z}$.
• Минимум $y = -1$ достигается в точках $x = \pi + 2k\pi$.
• Функция убывает на интервале $\left(0, \pi\right)$.
• Функция возрастает на интервале $\left(\pi, 2\pi\right)$.

Обозначения для отрезков и их монотонности

• Возрастает — функция идёт вверх, то есть $y$ увеличивается при увеличении $x$.
• Убывает — функция идёт вниз, то есть $y$ уменьшается при увеличении $x$.

Задача:

Определить поведение функции на заданных отрезках.

1) Отрезок $\left[\frac{\pi}{2}; \frac{3\pi}{2}\right]$

• График на этом отрезке:
  Рассмотрим точки:
  • $x = \frac{\pi}{2}$, $y = \cos \frac{\pi}{2} = 0$.
  • $x = \pi$, $y = \cos \pi = -1$ — минимум.
  • $x = \frac{3\pi}{2}$, $y = \cos \frac{3\pi}{2} = 0$.
• Поведение функции:
  • На отрезке $\left[\frac{\pi}{2}; \pi\right]$ функция убывает, так как от 0 до -1.
  • На отрезке $\left[\pi; \frac{3\pi}{2}\right]$ функция возрастает, так как от -1 до 0.

2) Отрезок $\left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$

• График на этом отрезке:
  • $x = -\frac{\pi}{2}$, $y = \cos \left(-\frac{\pi}{2}\right) = 0$.
  • $x = 0$, $y = \cos 0 = 1$ — максимум.
  • $x = \frac{\pi}{2}$, $y = 0$.
• Поведение функции:
  • На отрезке $\left[-\frac{\pi}{2}; 0\right]$ функция возрастает от 0 до 1.
  • На отрезке $\left[0; \frac{\pi}{2}\right]$ функция убывает от 1 до 0.

3) Отрезок $\left[0; \frac{3\pi}{2}\right]$

• График:
  • $x=0$, $y=1$.
  • $x=\pi$, $y=-1$.
  • $x=\frac{3\pi}{2}$, $y=0$.
• Поведение функции:
  • На отрезке $[0; \pi]$ функция убывает от 1 до -1.
  • На отрезке $\left[\pi; \frac{3\pi}{2}\right]$ функция возрастает от -1 до 0.

4) Отрезок $\left[-\pi; \frac{\pi}{2}\right]$

• График:
  • $x=-\pi$, $y = \cos(-\pi) = -1$.
  • $x=0$, $y=1$.
  • $x=\frac{\pi}{2}$, $y=0$.
• Поведение функции:
  • На отрезке $[- \pi; 0]$ функция возрастает от -1 до 1.
  • На отрезке $\left[0; \frac{\pi}{2}\right]$ функция убывает от 1 до 0.

Итог: