ГДЗ по Алгебре 10-11 Класс Номер 709 Алимов — Подробные Ответы

(Устно.) Выяснить, возрастает или убывает функция у = cos х на отрезке:

1. [3пи; 4пи];
2. [-2пи; -пи];
3. [2пи; 5пи/2];
4. [-пи/2; 0];
5. [1;3];
6. [-2;-1].

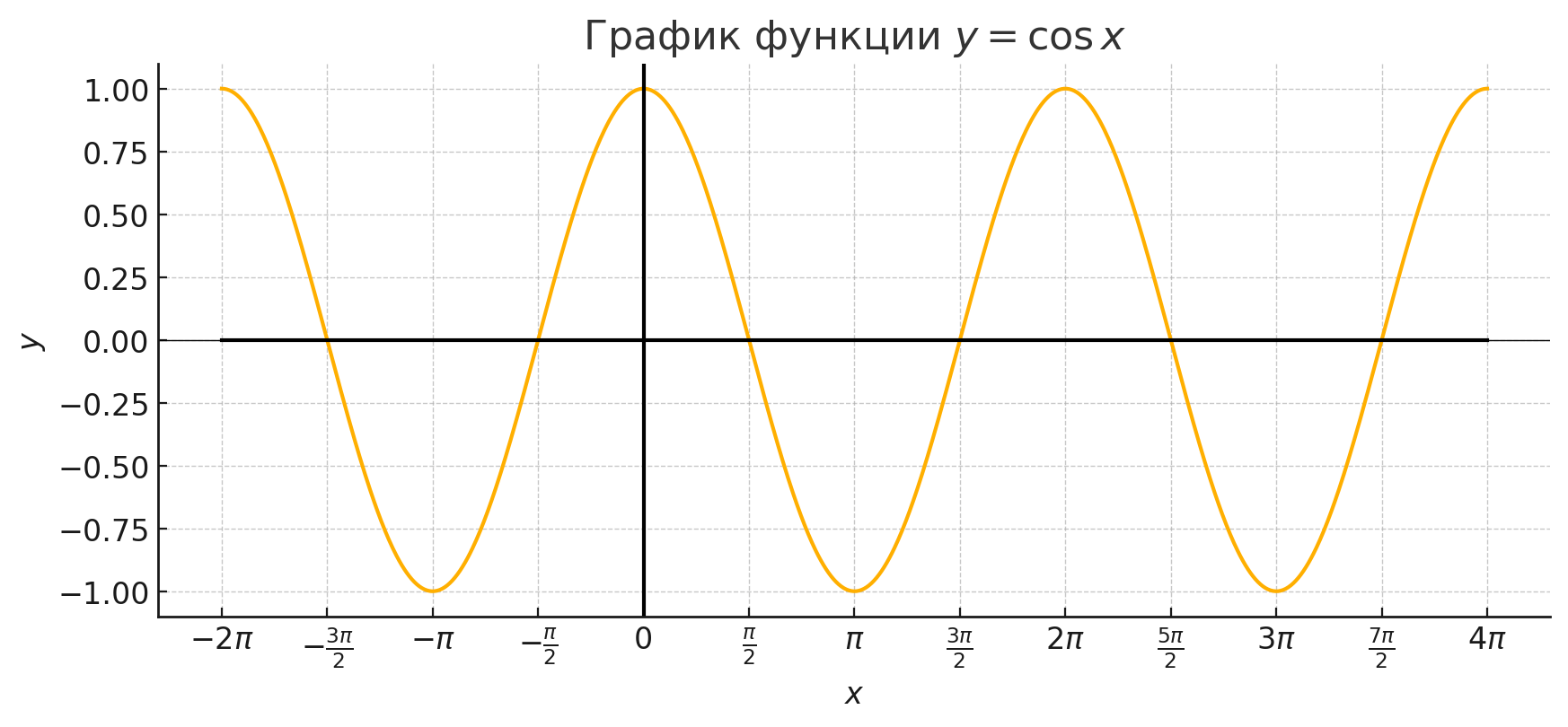
Воспользуемся графиком функции $y = \cos x$:

1. На отрезке $[3\pi; 4\pi]$ функция возрастает;
2. На отрезке $[-2\pi; -\pi]$ функция убывает;
3. На отрезке $\left[2\pi; \frac{5\pi}{2}\right]$ функция убывает;
4. На отрезке $\left[-\frac{\pi}{2}; 0\right]$ функция возрастает;
5. На отрезке $[1; 3]$ функция убывает;
6. На отрезке $[-2; -1]$ функция возрастает;

Используя график функции $y = \cos x$, определить, на каких указанных отрезках функция возрастает, а на каких — убывает.

Шаг 1. Вспомним свойства функции $y = \cos x$

• Функция $\cos x$ — это периодическая тригонометрическая функция с периодом $2\pi$.
• Максимумы функции равны 1, минимумы равны -1.
• Функция периодически колеблется между 1 и -1.
• График функции — волна, которая начинается на $x=0$ с максимума $\cos 0 = 1$.
• Между максимумом и минимумом функция убывает, между минимумом и максимумом — возрастает.
• Ключевые точки — это точки, где функция меняет поведение:
  • Максимумы при $x = 2k\pi$, где $k \in \mathbb{Z}$.
  • Минимумы при $x = (2k+1)\pi$.
  • Нули функции при $x = \frac{\pi}{2} + k\pi$.

Шаг 2. Анализ интервалов из задания

1) Интервал $[3\pi; 4\pi]$ — функция возрастает?

• Рассмотрим график и значения функции в этих точках:
  • $3\pi$ — это точка минимума функции (так как $3\pi = (2 \cdot 1 + 1)\pi$), здесь $\cos 3\pi = -1$.
  • $4\pi$ — это точка максимума функции (так как $4\pi = 2 \cdot 2 \pi$), здесь $\cos 4\pi = 1$.
• Между минимумом и следующим максимумом функция возрастает (график поднимается от -1 к 1).
• Вывод: На отрезке $[3\pi; 4\pi]$ функция действительно возрастает.

2) Интервал $[-2\pi; -\pi]$ — функция убывает?

• $-2\pi$ — максимум функции, так как $-2\pi = 2 \cdot (-1)\pi$, $\cos(-2\pi) = 1$.
• $-\pi$ — минимум функции, так как $-\pi = (2 \cdot (-1) + 1)\pi$, $\cos(-\pi) = -1$.
• Между максимумом и минимумом функция убывает (график опускается от 1 к -1).
• Вывод: На отрезке $[-2\pi; -\pi]$ функция убывает.

3) Интервал $\left[2\pi; \frac{5\pi}{2}\right]$ — функция убывает?

• $2\pi$ — максимум функции, $\cos 2\pi = 1$.
• $\frac{5\pi}{2} = 2\pi + \frac{\pi}{2}$ — это точка, где функция проходит через ноль (переходит от положительных значений к отрицательным).
• На интервале от максимума $2\pi$ до точки $\frac{5\pi}{2}$, функция убывает от 1 до 0.
• Вывод: На отрезке $\left[2\pi; \frac{5\pi}{2}\right]$ функция убывает.

4) Интервал $\left[-\frac{\pi}{2}; 0\right]$ — функция возрастает?

• $-\frac{\pi}{2}$ — это нулевая точка функции $\cos(-\frac{\pi}{2}) = 0$.
• $0$ — максимум функции, $\cos 0 = 1$.
• Между нулём и максимумом функция возрастает (график поднимается от 0 к 1).
• Вывод: На отрезке $\left[-\frac{\pi}{2}; 0\right]$ функция возрастает.

5) Интервал $[1; 3]$ — функция убывает?

• Этот интервал не кратен $\pi$, рассмотрим поведение функции на отрезке $x \in [1; 3]$.
• Проверим значения функции на концах:
  • $\cos 1 \approx 0.54$
  • $\cos 3 \approx -0.99$
• Видно, что функция убывает (с 0.54 до примерно -1).
• Проверим производную для уверенности:

$$\frac{d}{dx} \cos x = -\sin x$$

• На интервале $[1; 3]$:
  • При $x=1$, $\sin 1 > 0$, значит производная $-\sin 1 < 0$, функция убывает.
  • При $x=3$, $\sin 3 > 0$, производная отрицательна.
• Функция убывает на данном отрезке.
• Вывод: На отрезке $[1; 3]$ функция убывает.

6) Интервал $[-2; -1]$ — функция возрастает?

• Рассмотрим значения функции на концах:
  • $\cos(-2) = \cos 2 \approx -0.42$
  • $\cos(-1) = \cos 1 \approx 0.54$
• Видно, что функция возрастает (с -0.42 до 0.54).
• Проверим производную:

$$\frac{d}{dx} \cos x = -\sin x$$

• На интервале $[-2; -1]$:
  • При $x = -2$, $\sin(-2) = -\sin 2 < 0$, значит $-\sin(-2) = -(-\sin 2) = \sin 2 > 0$, производная положительна.
  • При $x = -1$, $\sin(-1) = -\sin 1 < 0$, значит производная положительна.
• Функция возрастает на данном отрезке.
• Вывод: На отрезке $[-2; -1]$ функция возрастает.

Итог: