ГДЗ по Алгебре 10-11 Класс Номер 708 Алимов — Подробные Ответы

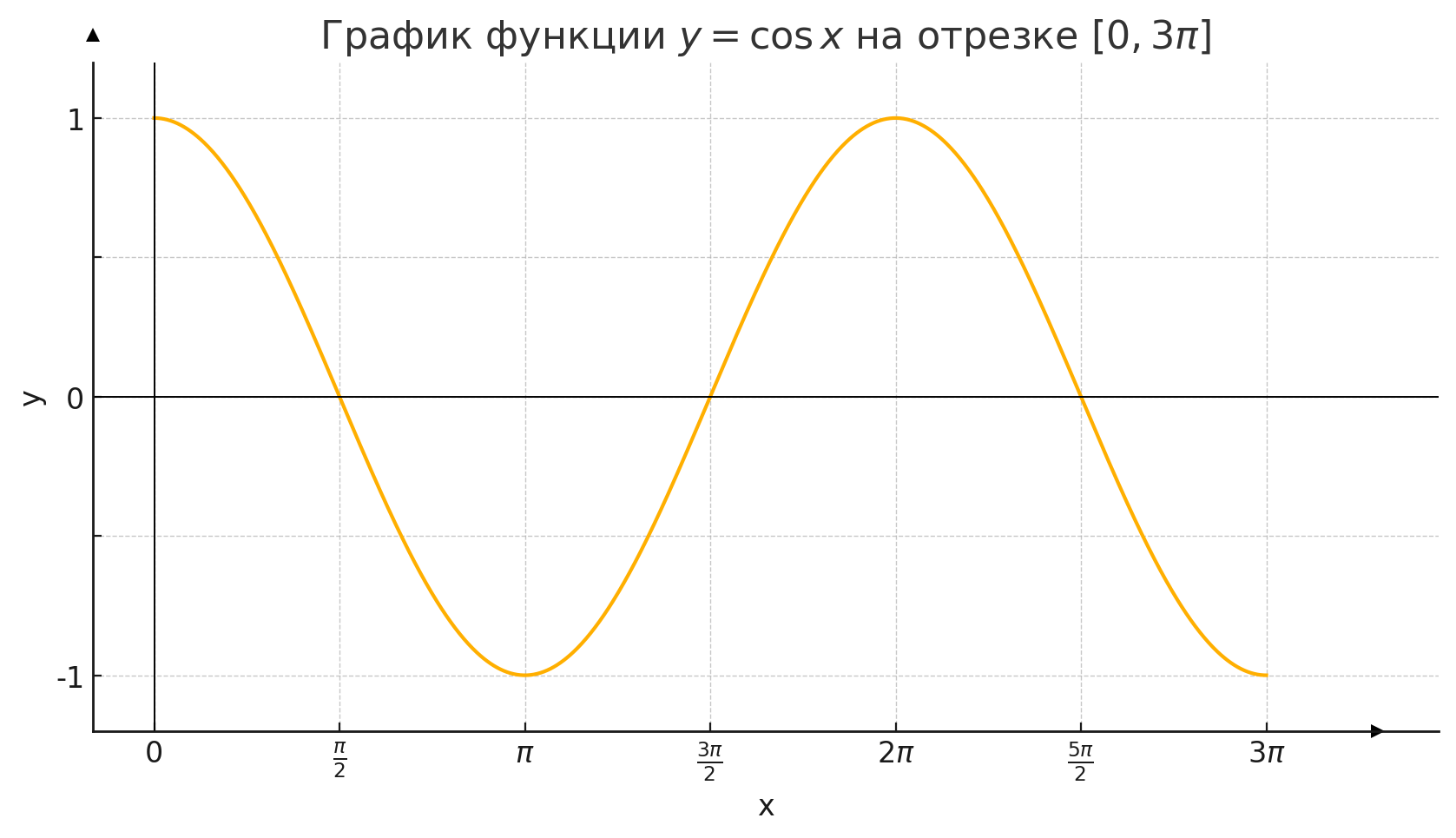
Пользуясь графиком функции у = cos х, выполнить упражнения (708—713).

(Устно.) Выяснить, при каких значениях ху принадлежащих отрезку [0; 3пи], функция у = cos х принимает:

1. значение, равное 0, 1, -1;
2. положительные значения;
3. отрицательные значения.

Воспользуемся графиком функции $y = \cos x$ на отрезке $[0; 3\pi]$:

1. Функция принимает значение, равное:

   $$y = 0 \text{ при } x = \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2};$$ $$y = 1 \text{ при } x = 0, 2\pi;$$ $$y = -1 \text{ при } x = \pi, 3\pi;$$

2. Функция принимает положительные значения при:

   $$0 < x < \frac{\pi}{2} \text{ и } \frac{3\pi}{2} < x < \frac{5\pi}{2};$$

3. Функция принимает отрицательные значения при:

   $$\frac{\pi}{2} < x < \frac{3\pi}{2} \text{ и } \frac{5\pi}{2} < x < 3\pi;$$

Дана функция $y = \cos x$ на отрезке $[0; 3\pi]$. Требуется исследовать поведение функции на этом отрезке, используя график.

Шаг 1. Построение графика функции $y = \cos x$

Функция $y = \cos x$ — это периодическая тригонометрическая функция, которая изменяется с периодом $2\pi$. Основные свойства:

• Период функции: $2\pi$.
• Амплитуда: 1 (максимальное значение функции равно 1, минимальное -1).
• Функция колеблется между значениями $-1$ и $1$.
• Значения функции в ключевых точках:
  • $\cos 0 = 1$,
  • $\cos \frac{\pi}{2} = 0$,
  • $\cos \pi = -1$,
  • $\cos \frac{3\pi}{2} = 0$,
  • $\cos 2\pi = 1$,
  • $\cos \frac{5\pi}{2} = 0$,
  • $\cos 3\pi = -1$.

На интервале $[0; 3\pi]$ функция совершает полных один с половиной периодов (т.к. $3\pi = 1.5 \cdot 2\pi$).

Шаг 2. Определение значений функции в важных точках

2.1. Когда функция равна нулю?

Функция $\cos x = 0$, когда аргумент равен $\frac{\pi}{2} + k\pi$, где $k \in \mathbb{Z}$.

На отрезке $[0, 3\pi]$ это:

• $x = \frac{\pi}{2}$ при $k=0$,
• $x = \frac{3\pi}{2}$ при $k=1$,
• $x = \frac{5\pi}{2}$ при $k=2$.

Значит, $y = 0$ при $x = \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}$.

2.2. Когда функция равна 1?

Функция $\cos x = 1$ при $x = 2k\pi$, $k \in \mathbb{Z}$.

На отрезке $[0, 3\pi]$ это:

• $x = 0$ (при $k=0$),
• $x = 2\pi$ (при $k=1$).

2.3. Когда функция равна -1?

Функция $\cos x = -1$ при $x = \pi + 2k\pi$, $k \in \mathbb{Z}$.

На отрезке $[0, 3\pi]$ это:

• $x = \pi$ (при $k=0$),
• $x = 3\pi$ (при $k=1$).

Шаг 3. Определение знака функции на промежутках

Функция $\cos x$ меняет знак в точках, где равна нулю, т.е. в $x = \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}$.

Проверим знак функции на каждом из промежутков, ограниченных этими точками:

• $(0, \frac{\pi}{2})$:
  Выберем тестовую точку, например, $x = \frac{\pi}{4}$.
  Тогда $\cos \frac{\pi}{4} = \frac{\sqrt{2}}{2} > 0$, значит на этом промежутке функция положительна.
• $(\frac{\pi}{2}, \frac{3\pi}{2})$:
  Выберем тестовую точку, например, $x = \pi$.
  $\cos \pi = -1 < 0$, значит на этом промежутке функция отрицательна.
• $(\frac{3\pi}{2}, \frac{5\pi}{2})$:
  Тестовая точка: $x = 2\pi$.
  $\cos 2\pi = 1 > 0$, функция положительна.
• $(\frac{5\pi}{2}, 3\pi)$:
  Тестовая точка: $x = \frac{11\pi}{4}$ (примерно 8.64).
  $\cos \frac{11\pi}{4} = \cos (2\pi + \frac{3\pi}{4}) = \cos \frac{3\pi}{4} = -\frac{\sqrt{2}}{2} < 0$, функция отрицательна.

Итоговое решение:

1) Значения функции:

$$y = 0 \text{ при } x = \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2};$$ $$y = 1 \text{ при } x = 0, 2\pi;$$ $$y = -1 \text{ при } x = \pi, 3\pi;$$

2) Положительные значения функции:

$$0 < x < \frac{\pi}{2} \quad \text{и} \quad \frac{3\pi}{2} < x < \frac{5\pi}{2};$$

3) Отрицательные значения функции:

$$\frac{\pi}{2} < x < \frac{3\pi}{2} \quad \text{и} \quad \frac{5\pi}{2} < x < 3\pi;$$