ГДЗ по Алгебре 10-11 Класс Номер 429 Алимов — Подробные Ответы

Отметить на единичной окружности точки, соответствующие числу а, если:

1. sina=1;
2. sin а = 0;
3. cosa = -1;
4. cos а = 0;
5. sin а = -0,6;
6. sin а = 0,5;
7. cosa=1/3.

Задание:

Отметить на единичной окружности точки, соответствующие числу $a$, если:

$\sin a = 1$;
Искомая точка имеет ординату, равную 1:

$\sin a = 0$;
Искомая точка имеет ординату, равную 0:

$\cos a = -1$;
Искомая точка имеет абсциссу, равную (-1):

$\cos a = 0$;
Искомая точка имеет абсциссу, равную 0:

$\sin a = -0.6$;
Искомая точка имеет ординату, равную (-0.6):

$\sin a = 0.5$;
Искомая точка имеет ординату, равную 0.5:

$\cos a = \frac{1}{3}$;
Искомая точка имеет абсциссу, равную $\frac{1}{3}$:

Задача:

Отметить на единичной окружности точки, соответствующие числу $a$, если заданы значения синуса или косинуса $a$.

Общее объяснение:

Единичная окружность — это окружность с радиусом 1, центр которой находится в начале координат $(0,0)$ на координатной плоскости.

• Координаты точки на этой окружности можно записать как $(\cos a, \sin a)$, где $a$ — угол в радианах от положительного направления оси $x$ (абсциссы).
• $\cos a$ — абсцисса (координата по оси $x$) точки на окружности.
• $\sin a$ — ордината (координата по оси $y$) точки на окружности.

Поэтому, чтобы найти точку на единичной окружности, соответствующую углу $a$, мы используем эти значения.

Подробное решение каждого случая:

1) $\sin a = 1$

• Нам дано: ордината точки $y = \sin a = 1$.
• На единичной окружности максимальное значение ординаты — 1, оно достигается в верхней точке окружности.
• Следовательно, точка находится в координате:

  $$(x, y) = (\cos a, \sin a) = (0, 1)$$

• На окружности это точка на вершине, на оси $y$.

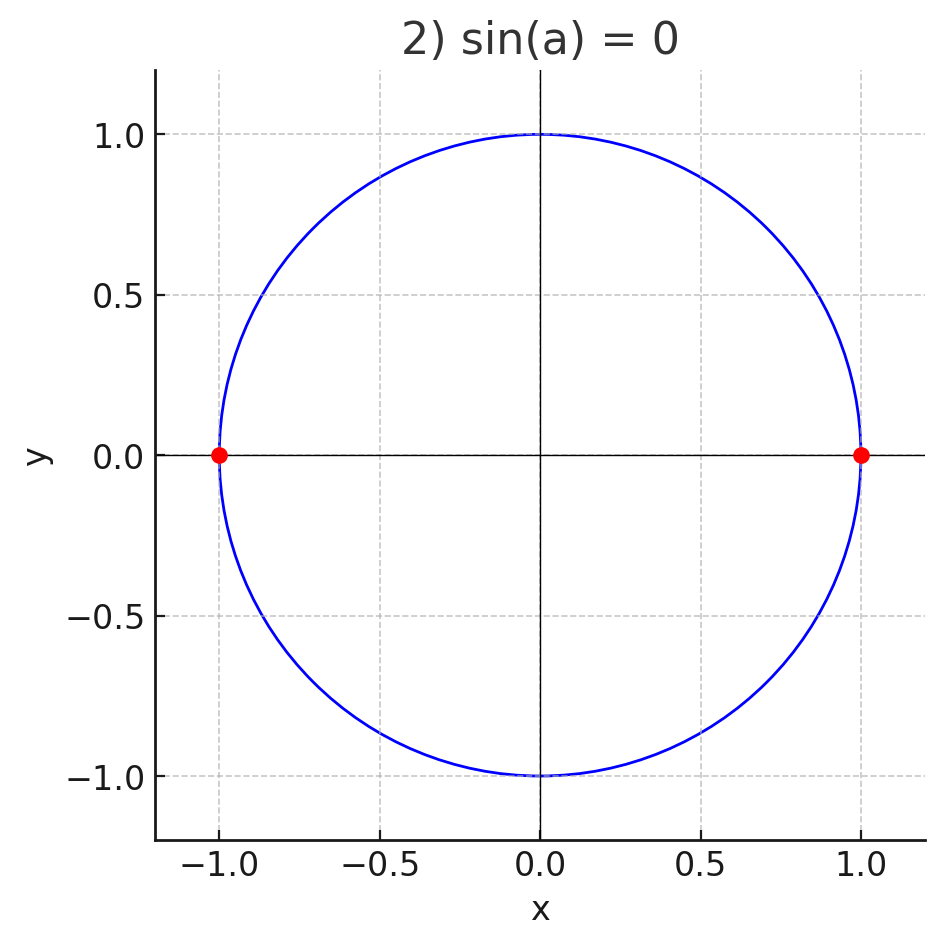
2) $\sin a = 0$

• Нам дано: $\sin a = 0$.
• Значение синуса равно нулю в тех точках окружности, где ордината равна 0 — это точки на оси $x$.
• Тогда точки имеют координаты:

  $$(1, 0) \quad \text{и} \quad (-1, 0)$$

• Эти точки — правый и левый концы окружности на оси $x$.

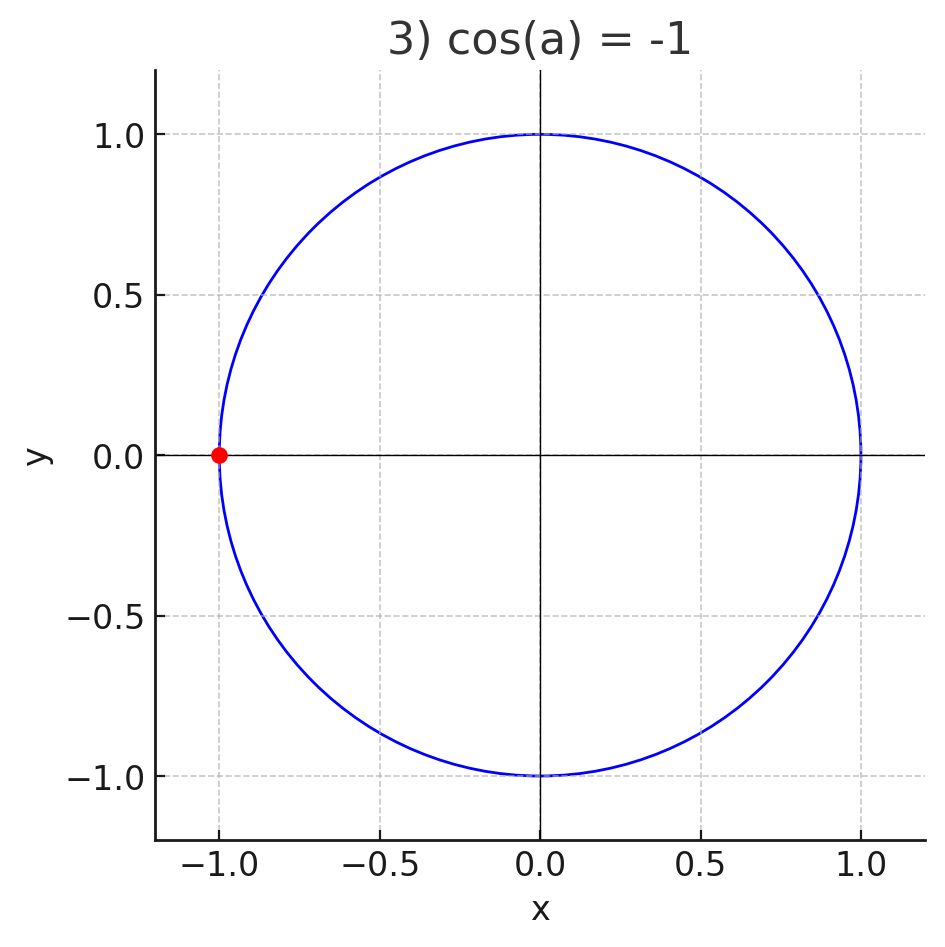
3) $\cos a = -1$

• Нам дано: $\cos a = -1$.
• Косинус — это абсцисса, равная -1, значит точка находится в крайней левой точке окружности.
• Координаты точки:

  $$(x, y) = (-1, 0)$$

• Точка лежит на оси $x$, слева от центра.

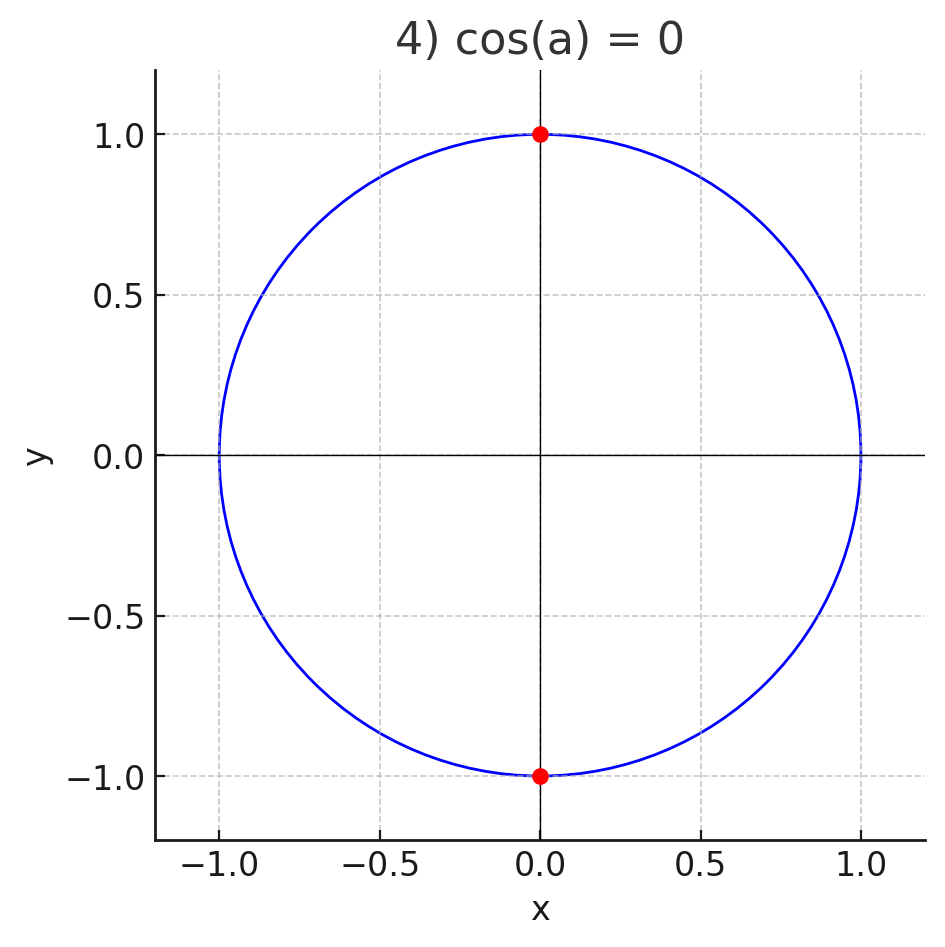
4) $\cos a = 0$

• Дано: $\cos a = 0$.
• Значение косинуса равно нулю в точках, где абсцисса равна 0 — это точки на оси $y$.
• На единичной окружности такие точки:

  $$(0, 1) \quad \text{и} \quad (0, -1)$$

• Верхняя и нижняя точки окружности на оси $y$.

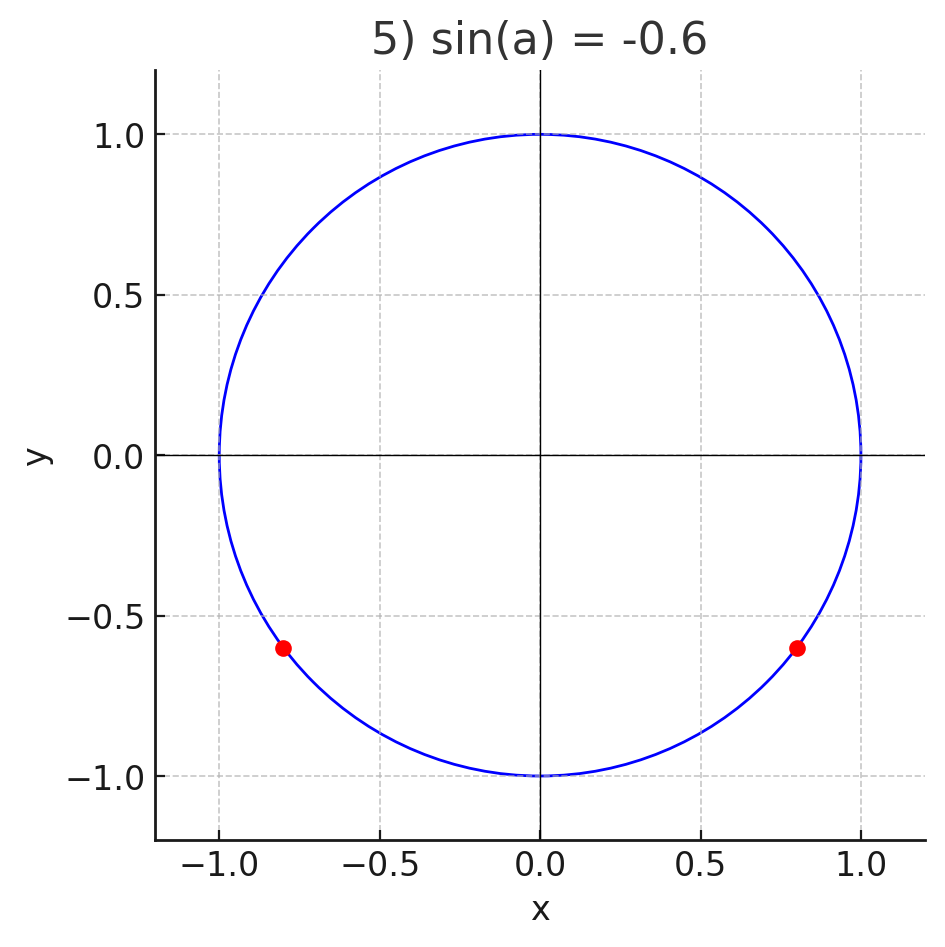
5) $\sin a = -0.6$

• Дано: $\sin a = -0.6$.
• Ордината точки равна -0.6 — это ниже оси $x$.
• Чтобы найти $x = \cos a$, используем уравнение окружности:

  $$x^2 + y^2 = 1^2 = 1$$

• Подставляем $y = -0.6$:

  $$x^2 + (-0.6)^2 = 1 \Rightarrow x^2 + 0.36 = 1 \Rightarrow x^2 = 0.64 \Rightarrow x = \pm 0.8$$

• Значит точки:

  $$(0.8, -0.6) \quad \text{и} \quad (-0.8, -0.6)$$

• Обе точки лежат на окружности, с ординатой -0.6.

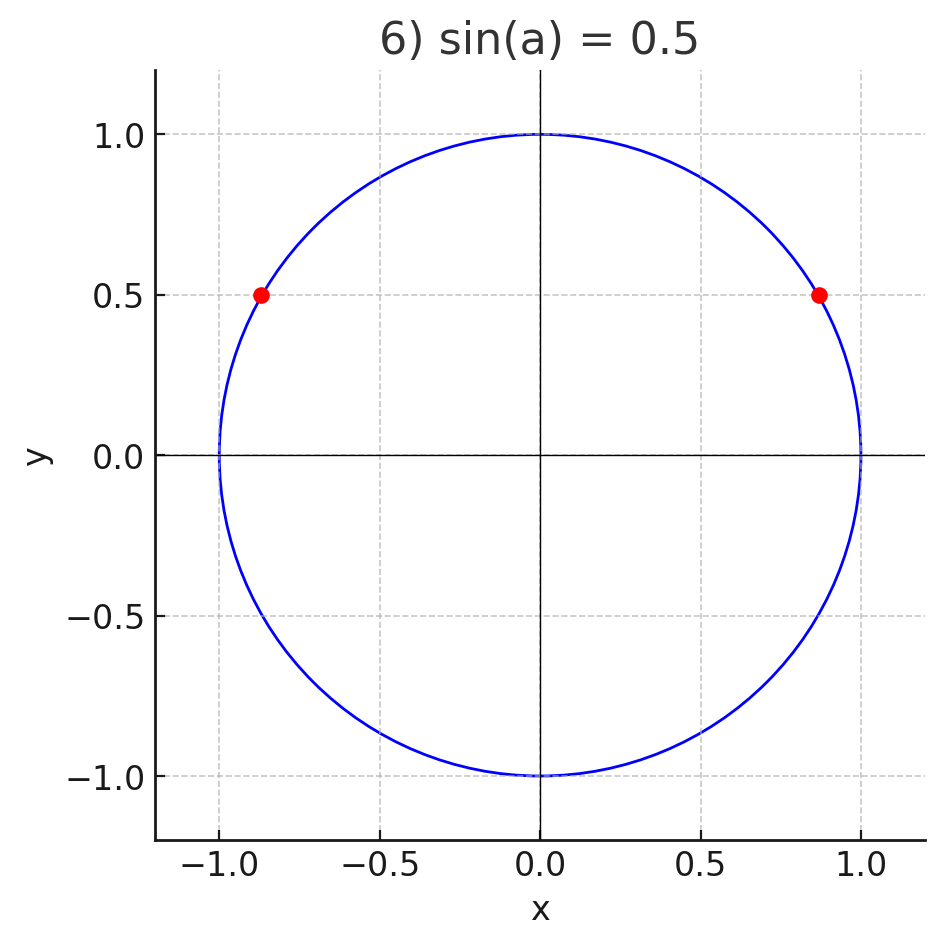
6) $\sin a = 0.5$

• Дано: $\sin a = 0.5$.
• Ордината равна 0.5 — выше оси $x$.
• Используем уравнение окружности:

  $$x^2 + (0.5)^2 = 1 \Rightarrow x^2 + 0.25 = 1 \Rightarrow x^2 = 0.75 \Rightarrow x = \pm \sqrt{0.75} \approx \pm 0.866$$

• Точки:

  $$(0.866, 0.5) \quad \text{и} \quad (-0.866, 0.5)$$

• Обе точки на окружности с заданной ординатой.

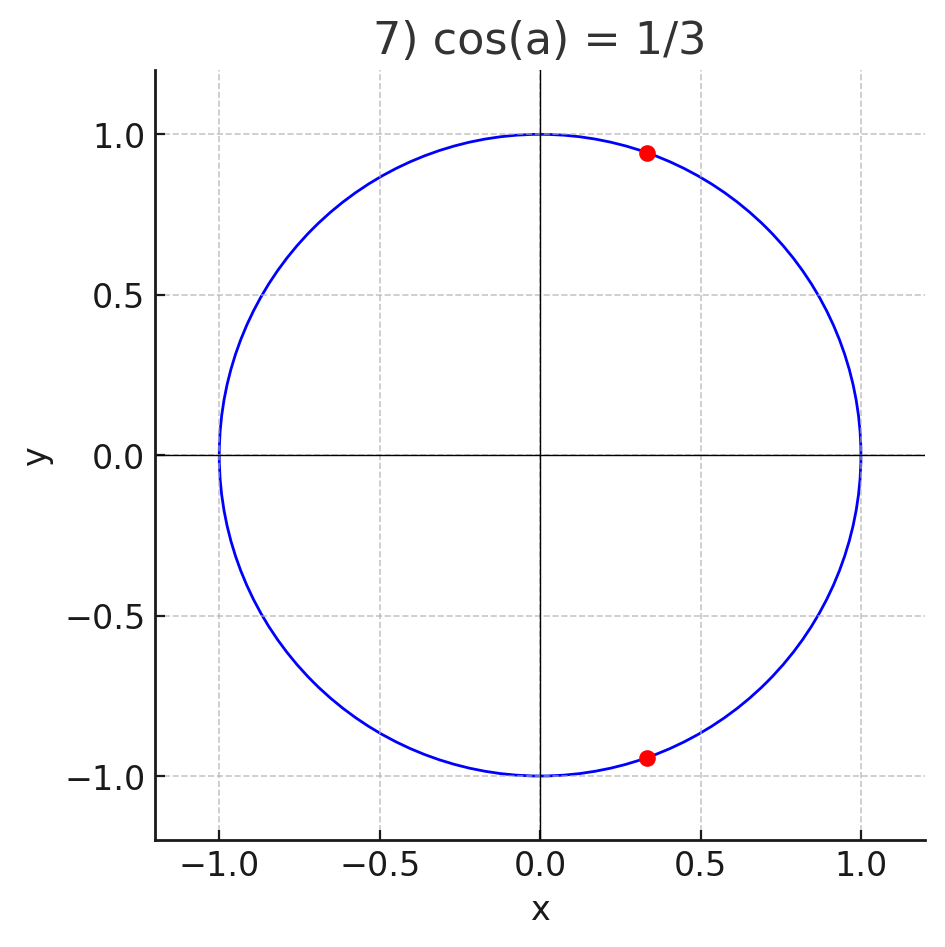
7) $\cos a = \frac{1}{3}$

• Дано: $\cos a = \frac{1}{3} \approx 0.3333$.
• Абсцисса равна $\frac{1}{3}$.
• Найдём ординату $y = \sin a$ из уравнения окружности:

  $$\left(\frac{1}{3}\right)^2 + y^2 = 1 \Rightarrow \frac{1}{9} + y^2 = 1 \Rightarrow y^2 = 1 — \frac{1}{9} = \frac{8}{9} \Rightarrow y = \pm \frac{2\sqrt{2}}{3} \approx \pm 0.9428$$

• Точки:

  $$\left(\frac{1}{3}, \frac{2\sqrt{2}}{3}\right) \quad \text{и} \quad \left(\frac{1}{3}, -\frac{2\sqrt{2}}{3}\right)$$

• Обе точки лежат на окружности с заданной абсциссой.

Итог:

В каждом случае нам нужно было:

1. Определить, какая координата известна (абсцисса или ордината).
2. Использовать уравнение единичной окружности $x^2 + y^2 = 1$ для вычисления неизвестной координаты.
3. Найти одну или две точки на окружности, удовлетворяющие заданному условию.