
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 426 Алимов — Подробные Ответы
На единичной окружности построить точку, полученную поворотом точки Р (1; 0) на угол:
- 4,5пи;
- 5,5пи;
- -6пи;
- -7пи.
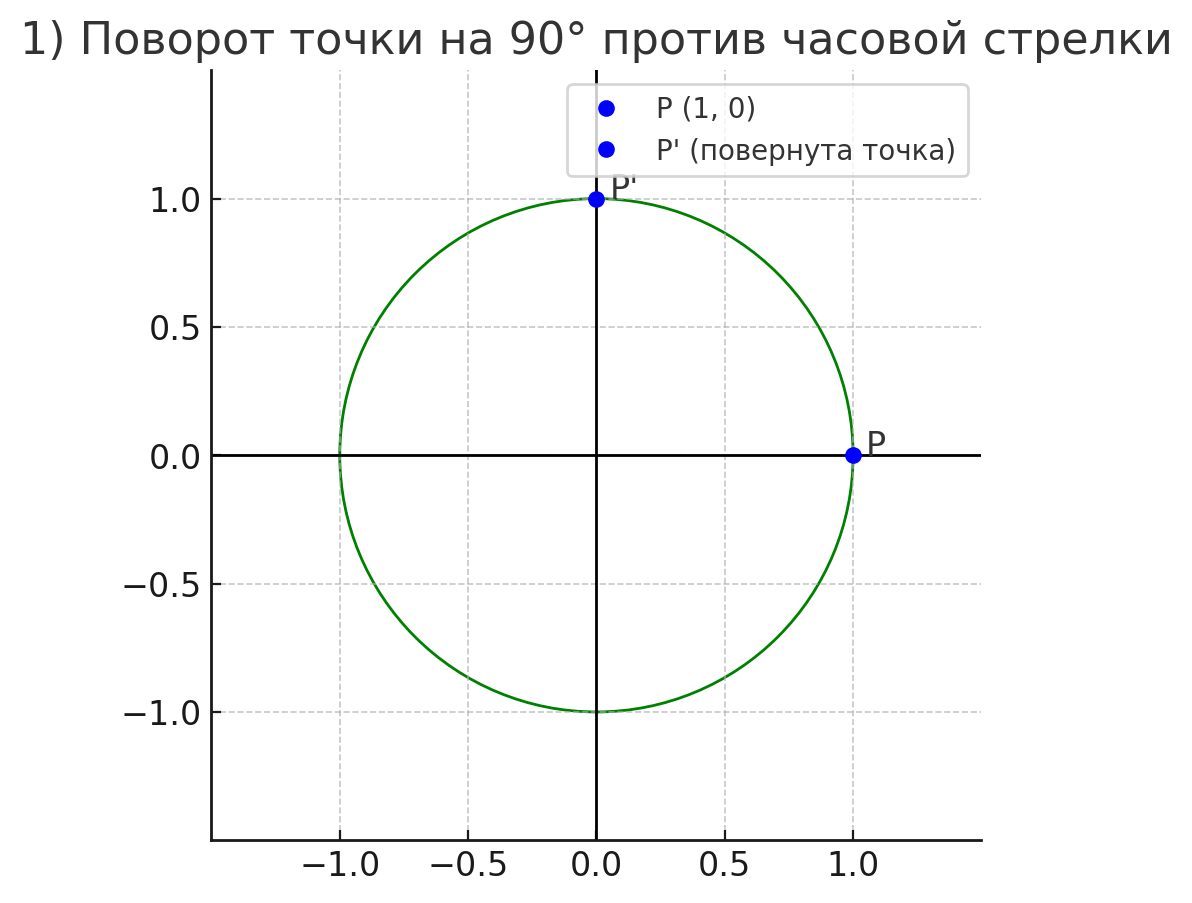
1) ;
;
Точка повернется на угол , против часовой стрелки:
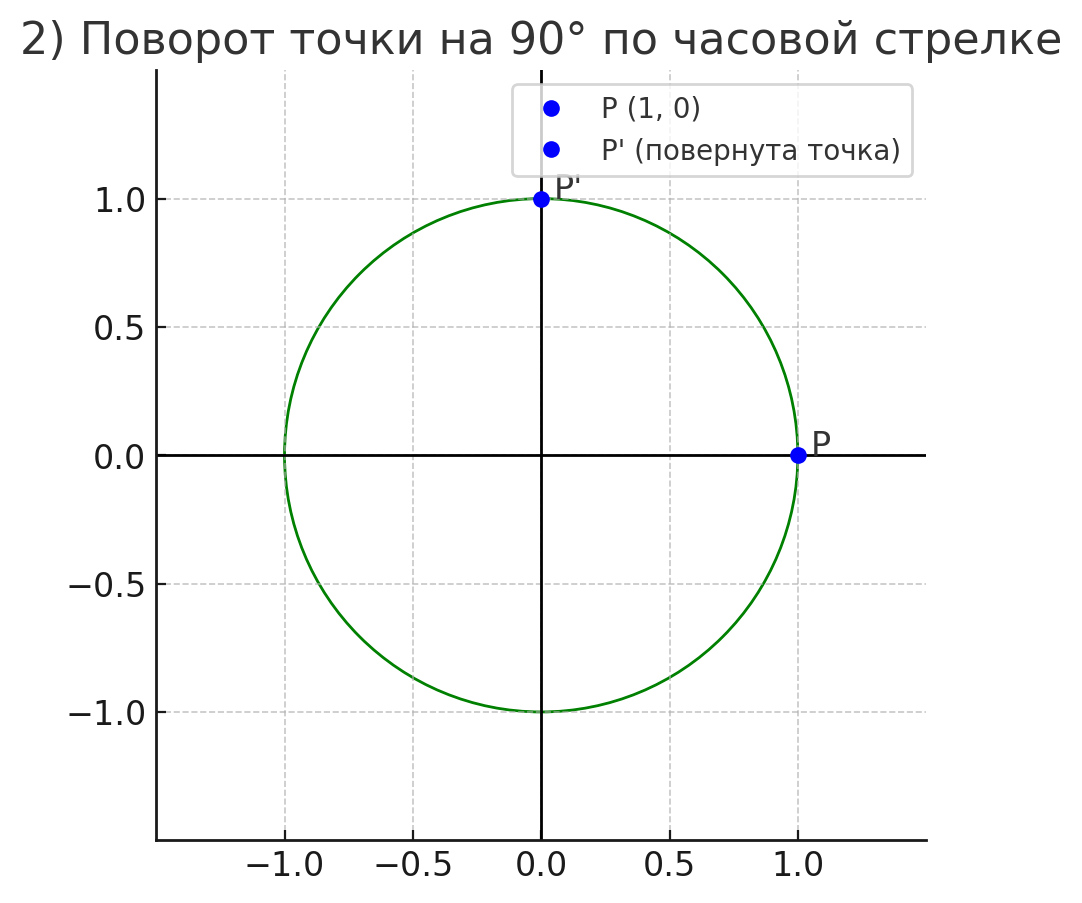
2) ;
;
;
Точка повернется на угол , по часовой стрелке:
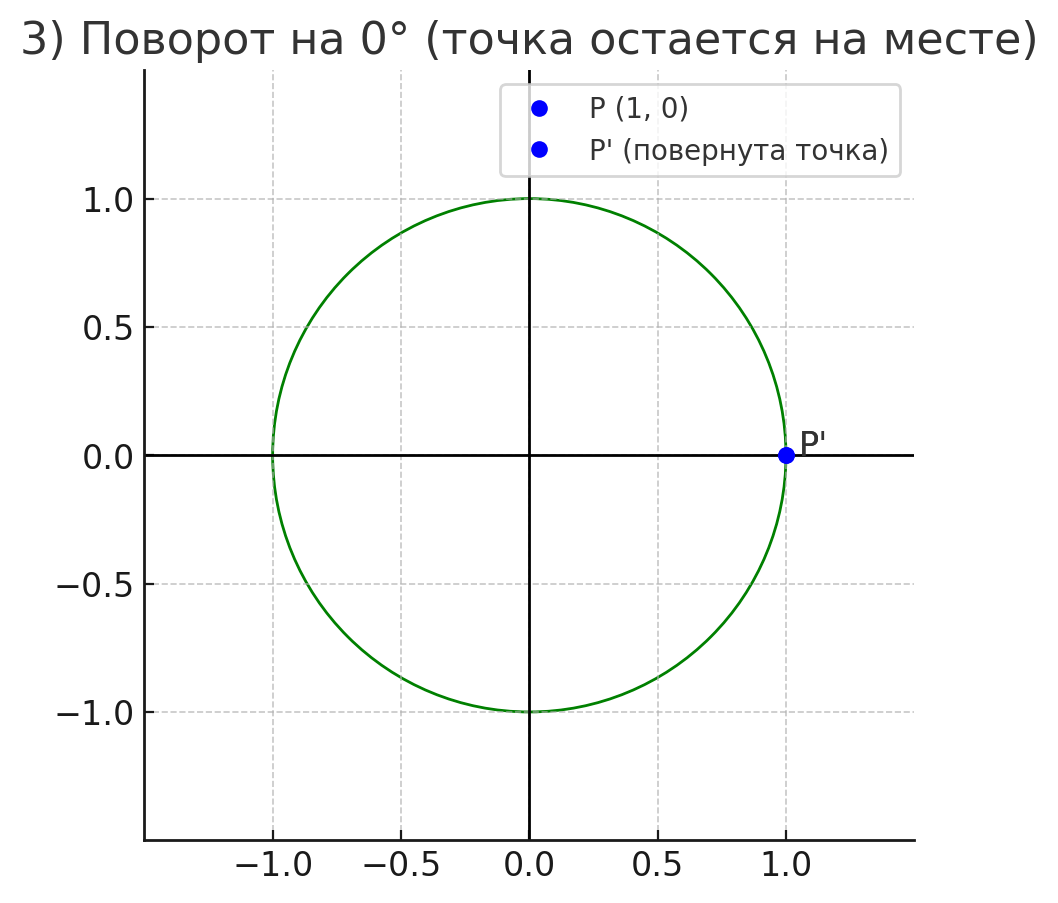
3) ;
;
Точка останется на прежнем месте:
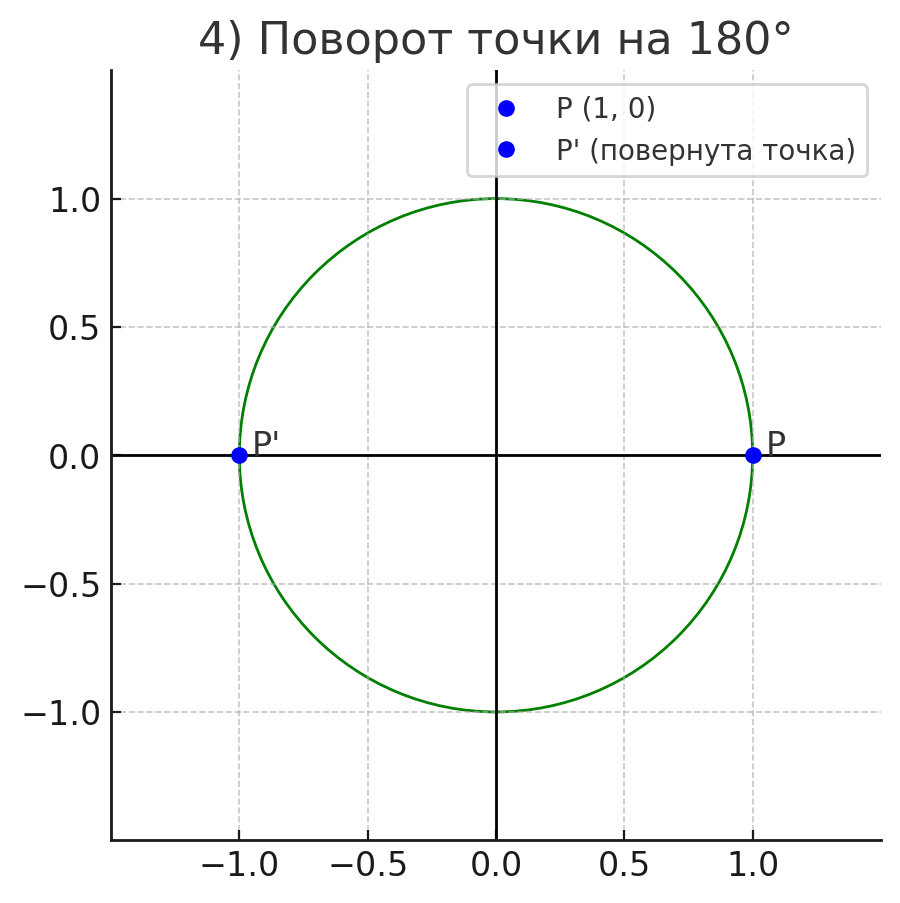
4) ;
;
Точка повернется на угол :
Условие задачи:
На единичной окружности построить точку, полученную поворотом точки на угол .
Основная идея:
Точка лежит на единичной окружности, значит её координаты при угле относительно положительного направления оси задаются:
В исходном положении точка находится на угле (то есть ).
Нам нужно повернуть точку на угол (в радианах) и найти новые координаты точки после поворота:
Объяснение задачи и как считать угол :
Часто угол задается большим числом, превышающим , или отрицательным. Поскольку поворот на (360°) — это полный оборот, который возвращает точку на то же место, то угол можно привести к эквивалентному углу на промежутке или , убрав целые обороты.
Подробное решение для каждого из случаев:
1)
- — это полных оборота (каждый оборот ).
- Угол поворота можно свести к .
Переводим радианы в градусы:
Это значит, что точка поворачивается на против часовой стрелки (положительное направление углов — против часовой стрелки).
Новые координаты точки :
То есть точка переместилась с в верхнюю точку окружности.
2)
- Аналогично, — это два полных оборота.
- Значит, можно рассмотреть угол
Переводим в градусы:
Это угол в градусах, но 270° — это поворот против часовой стрелки на , что эквивалентно повороту по часовой стрелке на
Значит точка поворачивается на по часовой стрелке.
Новые координаты точки :
Поворот по часовой стрелке на (или на в радианах):
Точка переместилась в нижнюю точку окружности.
3)
Здесь:
- Угол поворота — (три полных оборота по часовой стрелке).
- Так как полный оборот — , мы можем свести угол к
Точка не изменит положение, так как три полных оборота возвращают её в начальную точку:
4)
Приведём угол к эквивалентному:
- Вычитаем полные обороты , останется
Перевод в градусы:
Точка повернется на (против часовой стрелки или по часовой — неважно, результат одинаков):
Новые координаты точки :
Точка переместилась в противоположную точку окружности слева.
Итог:
| № | Угол | Приведённый угол | Направление поворота | Координаты |
|---|---|---|---|---|
| 1 | против часовой стрелки | |||
| 2 | по часовой стрелке | |||
| 3 | нет изменения | |||
| 4 | поворот на |



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!