ГДЗ по Алгебре 10-11 Класс Номер 418 Алимов — Подробные Ответы

1. пи/4+-2пи;
2. -пи/3+-2пи;
3. 2пи/3+-6пи;
4. -3пи/4+-8пи.

1) $\alpha = \frac{\pi}{4} \pm 2\pi$;

$a_0 = \frac{\pi}{4} = \left( \frac{180}{\pi} \cdot \frac{\pi}{4} \right)^{\circ} = \left( \frac{180}{4} \right)^{\circ} = 45^{\circ};$

Точка $P$ повернется на угол $45^\circ$, против часовой стрелки

2) $\alpha = -\frac{\pi}{3} \pm 2\pi$;

$a_0 = -\frac{\pi}{3} = -\left( \frac{180}{\pi} \cdot \frac{\pi}{3} \right)^{\circ} = -\left( \frac{180}{3} \right)^{\circ} = -60^{\circ};$

Точка $P$ повернется на угол $60^\circ$, по часовой стрелке

3) $\alpha = \frac{2\pi}{3} \pm 6\pi$;

$a_0 = \frac{2\pi}{3} = \left( \frac{180}{\pi} \cdot \frac{2\pi}{3} \right)^{\circ} = (60 \cdot 2)^{\circ} = 120^{\circ};$

Точка $P$ повернется на угол $120^\circ$, против часовой стрелки

4) $\alpha = -\frac{3\pi}{4} \pm 8\pi$;

$a_0 = -\frac{3\pi}{4} = -\left( \frac{180}{\pi} \cdot \frac{3\pi}{4} \right)^{\circ} = -(45 \cdot 3)^{\circ} = -135^{\circ};$

Точка $P$ повернется на угол $135^\circ$, по часовой стрелке

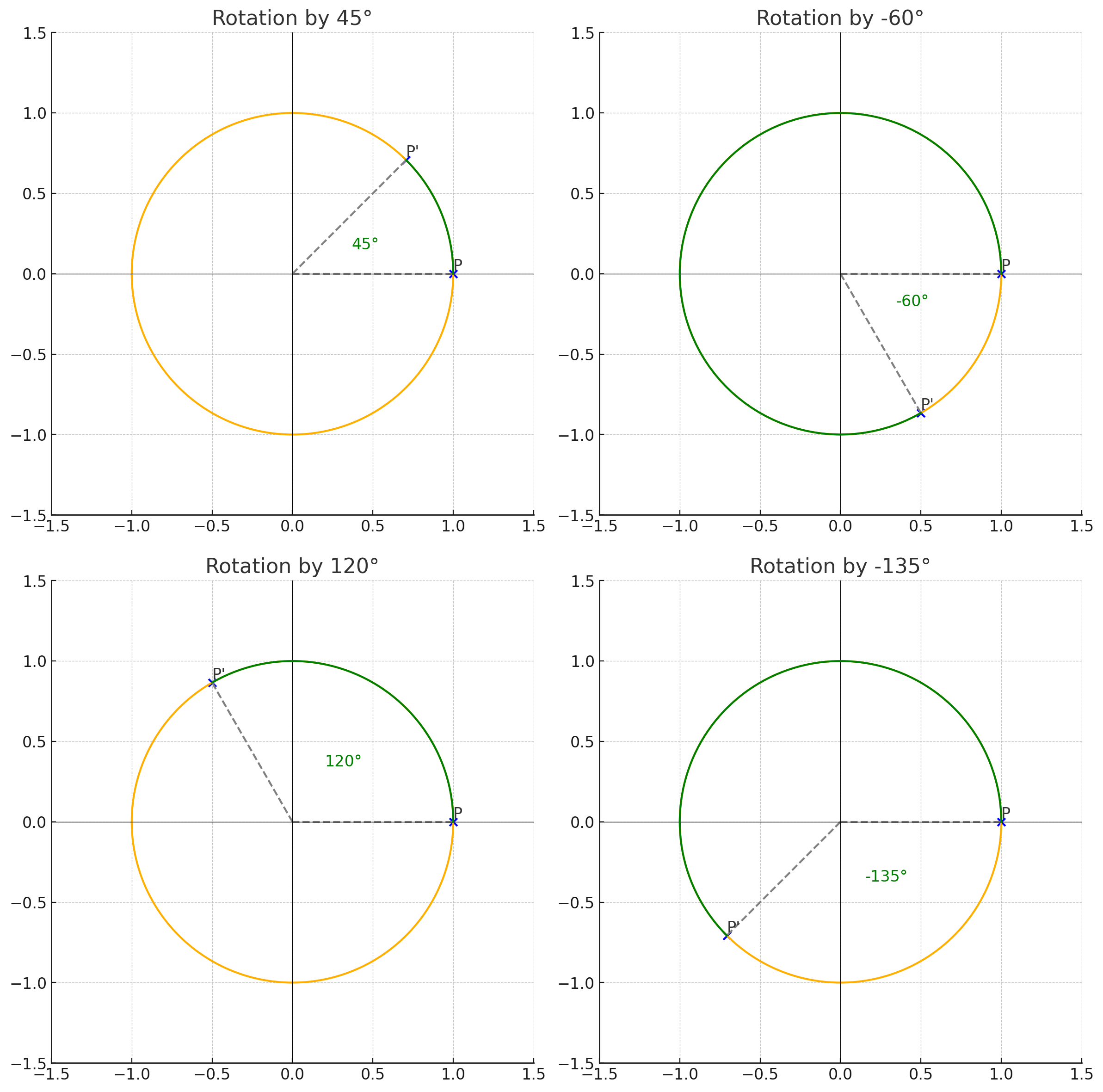
На единичной окружности построить точку, полученную поворотом точки $P(1; 0)$ на угол $\alpha$:

Введение и постановка задачи:

Дано: точка $P$ на единичной окружности, с координатами $P(1; 0)$. Это точка на оси $x$ (радиус 1, угол 0).

Нужно: найти новую точку, которая получается при повороте точки $P$ вокруг начала координат на угол $\alpha$.

Что значит поворот точки на угол $\alpha$?

• Единичная окружность — это окружность с центром в начале координат $O(0; 0)$ и радиусом 1.
• Начальная точка $P(1; 0)$ расположена на окружности на угле 0 радиан (или 0°).
• Поворот точки на угол $\alpha$ — это смещение точки по дуге окружности на угол $\alpha$.
• Положительный угол поворота считается против часовой стрелки.
• Отрицательный угол поворота — по часовой стрелке.

Математическое описание поворота

Пусть:

• $\alpha$ — угол поворота в радианах.
• Начальные координаты точки $P = (x_0, y_0) = (1, 0)$.
• Новые координаты $P’ = (x’, y’)$ после поворота на угол $\alpha$ вокруг начала координат определяются формулами:

$$x’ = x_0 \cos \alpha — y_0 \sin \alpha = \cos \alpha,$$ $$y’ = x_0 \sin \alpha + y_0 \cos \alpha = \sin \alpha.$$

Так как $y_0 = 0$, формулы упрощаются.

Рассмотрим каждый случай по отдельности.

1) Угол:

$$\alpha = \frac{\pi}{4} \pm 2\pi.$$

Что значит $\pm 2\pi$?

• Угол $2\pi$ радиан — это полный оборот вокруг окружности (360°).
• Поскольку поворот на полный круг не меняет положение точки, углы, отличающиеся на $2\pi$, эквивалентны.
• Значит $\alpha$ эквивалентен $\frac{\pi}{4}$.

Перевод угла в градусы:

$$a_0 = \frac{\pi}{4} \quad \Rightarrow \quad a_0 = \frac{180}{\pi} \times \frac{\pi}{4} = \frac{180}{4} = 45^\circ.$$

Направление поворота:

• Положительный угол $+\frac{\pi}{4}$ — поворот против часовой стрелки.
• Значит точка $P$ повернется на угол 45° против часовой стрелки.

Координаты новой точки:

$$x’ = \cos \frac{\pi}{4} = \frac{\sqrt{2}}{2} \approx 0.707,$$ $$y’ = \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} \approx 0.707.$$

Итог для 1):

Точка после поворота: $P’ \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$.

2) Угол:

$$\alpha = -\frac{\pi}{3} \pm 2\pi.$$

Аналогично, $\pm 2\pi$ не меняют положения.

Перевод угла в градусы:

$$a_0 = -\frac{\pi}{3} = -\frac{180}{\pi} \times \frac{\pi}{3} = -\frac{180}{3} = -60^\circ.$$

Направление поворота:

• Отрицательный угол — поворот по часовой стрелке.
• Значит точка $P$ повернется на 60° по часовой стрелке.

Координаты новой точки:

$$x’ = \cos \left(-\frac{\pi}{3}\right) = \cos \frac{\pi}{3} = \frac{1}{2} = 0.5,$$ $$y’ = \sin \left(-\frac{\pi}{3}\right) = -\sin \frac{\pi}{3} = -\frac{\sqrt{3}}{2} \approx -0.866.$$

Итог для 2):

Точка после поворота: $P’ \left(0.5, -\frac{\sqrt{3}}{2}\right)$.

3) Угол:

$$\alpha = \frac{2\pi}{3} \pm 6\pi.$$

Почему $\pm 6\pi$?

• $6\pi$ — это три полных оборота (3 × 360°).
• Значит поворот эквивалентен углу $\frac{2\pi}{3}$.

Перевод угла в градусы:

$$a_0 = \frac{2\pi}{3} = \frac{180}{\pi} \times \frac{2\pi}{3} = 60 \times 2 = 120^\circ.$$

Направление поворота:

• Положительный угол — против часовой стрелки.
• Значит поворот на 120° против часовой стрелки.

Координаты новой точки:

$$x’ = \cos \frac{2\pi}{3} = \cos 120^\circ = -\frac{1}{2} = -0.5,$$ $$y’ = \sin \frac{2\pi}{3} = \sin 120^\circ = \frac{\sqrt{3}}{2} \approx 0.866.$$

Итог для 3):

Точка после поворота: $P’ \left(-0.5, \frac{\sqrt{3}}{2}\right)$.

4) Угол:

$$\alpha = -\frac{3\pi}{4} \pm 8\pi.$$

Почему $\pm 8\pi$?

• $8\pi$ — это 4 полных оборота (4 × 360°).
• Значит поворот эквивалентен углу $-\frac{3\pi}{4}$.

Перевод угла в градусы:

$$a_0 = -\frac{3\pi}{4} = -\frac{180}{\pi} \times \frac{3\pi}{4} = -45 \times 3 = -135^\circ.$$

Направление поворота:

• Отрицательный угол — по часовой стрелке.
• Значит поворот на 135° по часовой стрелке.

Координаты новой точки:

$$x’ = \cos \left(-\frac{3\pi}{4}\right) = \cos \frac{3\pi}{4} = -\frac{\sqrt{2}}{2} \approx -0.707,$$ $$y’ = \sin \left(-\frac{3\pi}{4}\right) = -\sin \frac{3\pi}{4} = -\frac{\sqrt{2}}{2} \approx -0.707.$$

Итог для 4):

Точка после поворота: $P’ \left(-\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right)$.

Общий вывод:

• Поворот точки $P(1; 0)$ на угол $\alpha$ вокруг начала координат переводит её в точку с координатами:

$$P’ = (\cos \alpha, \sin \alpha).$$

• Углы, отличающиеся на целое число оборотов $2\pi$, задают одну и ту же точку.
• Положительные углы — поворот против часовой стрелки, отрицательные — по часовой стрелке.