ГДЗ по Алгебре 10-11 Класс Номер 376 Алимов — Подробные Ответы

Решить графически уравнение:

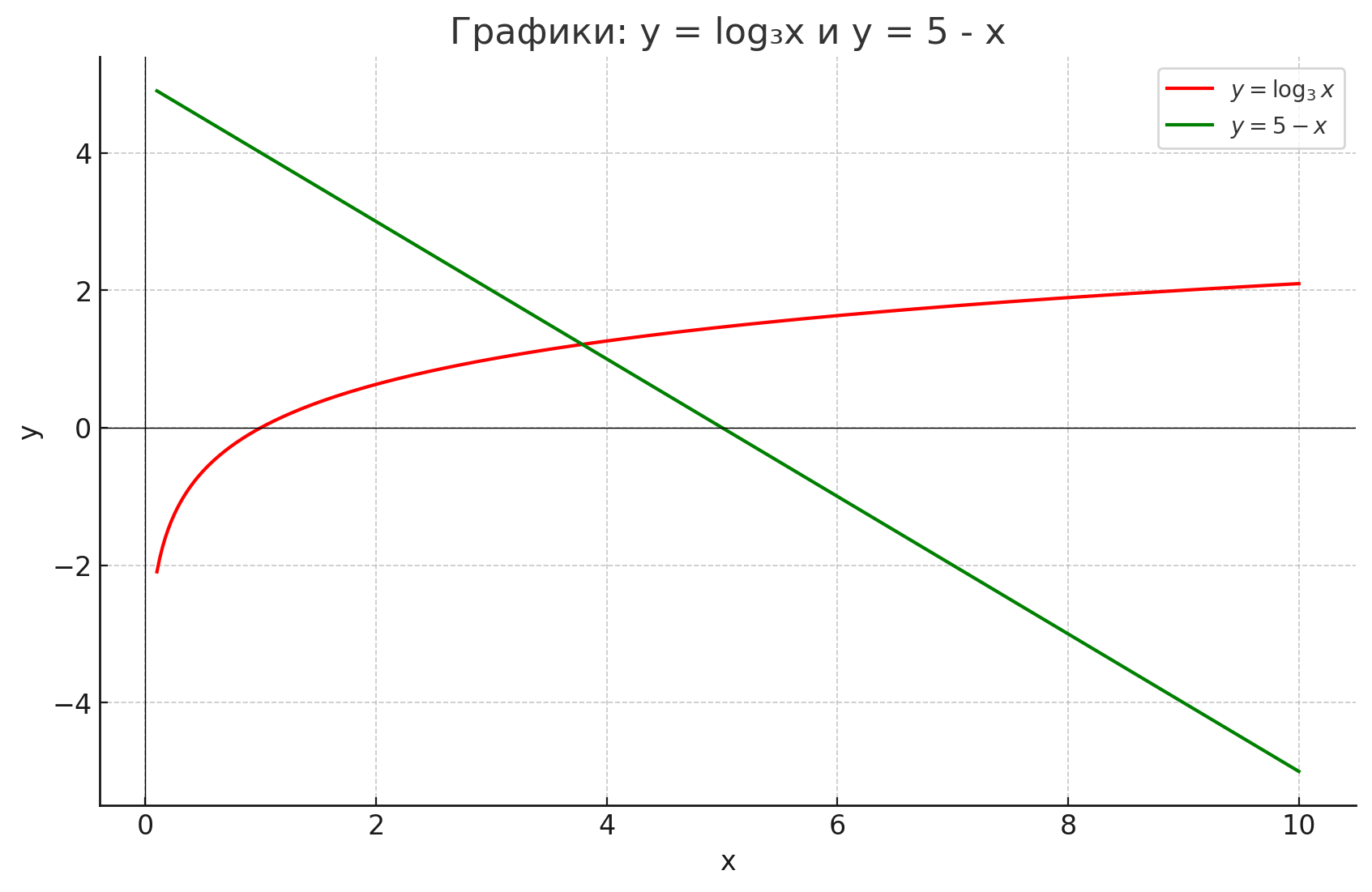
1. log3(x) = 5 — x;
2. log1/3(х) = 3x.

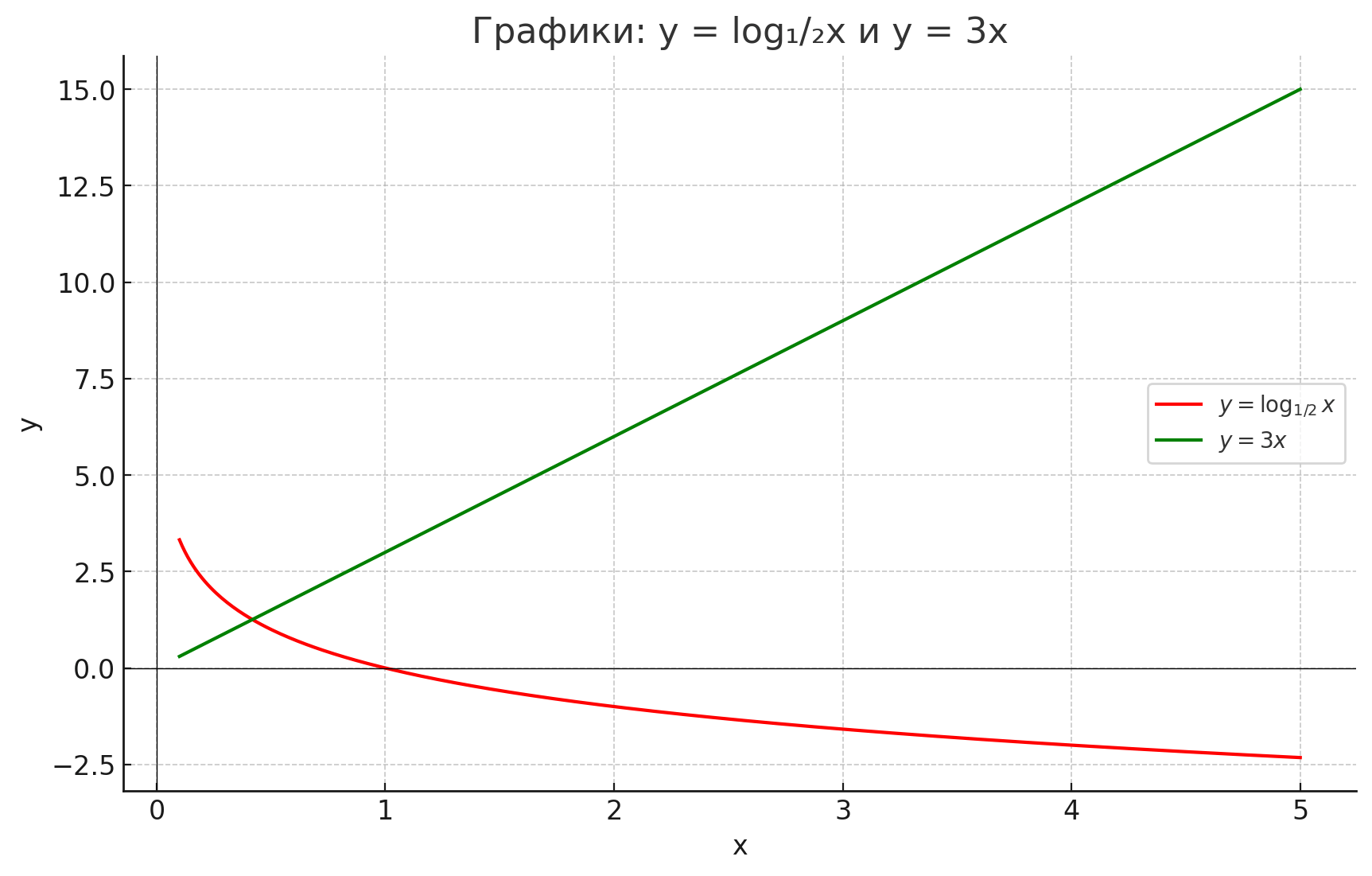
$\log_{3} x = 5 — x$;

$y = \log_{3} x$ — логарифмическая функция:

$y = 5 — x$ — уравнение прямой:

Графики функций:

Ответ: $x \approx 3,8$.

$\log_{\frac{1}{2}} x = 3x$;

$y = \log_{\frac{1}{2}} x$ — логарифмическая функция:

$y = 3x$ — уравнение прямой:

Графики функций:

Ответ: $x = \frac{1}{3}$.

1) Решить уравнение:

$$\log_3 x = 5 — x$$

Шаг 1: Понять структуру уравнения

Уравнение содержит:

• Логарифмическую функцию: $y = \log_3 x$
• Линейную функцию: $y = 5 — x$

Найти такое значение $x$, при котором обе функции дают одинаковый результат.

Шаг 2: Построим график каждой функции

Функция 1: $y = \log_3 x$

Это логарифмическая функция с основанием $a = 3 > 1$, поэтому:

• Область определения: $x > 0$
• Функция возрастает
• Проходит через точку $(1, 0)$, так как $\log_3 1 = 0$
• Значения:

  $$\begin{array}{|c|c|c|c|} \hline x & 1 & 3 & 9 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

Функция 2: $y = 5 — x$

Это прямая линия, убывающая. Построим по двум точкам:

• Если $x = 0$, то $y = 5$
• Если $x = 5$, то $y = 0$

$$\begin{array}{|c|c|c|} \hline x & 0 & 5 \\ \hline y & 5 & 0 \\ \hline \end{array}$$

Шаг 3: Графическое решение

На графике видно:

• Красная кривая: $y = \log_3 x$
• Зелёная прямая: $y = 5 — x$
• Они пересекаются примерно в точке $x \approx 3.8$

Шаг 4: Проверка приближённого значения

Найдём $\log_3 3.8$:

$$\log_3 3.8 = \frac{\log_{10} 3.8}{\log_{10} 3} \approx \frac{0.5798}{0.4771} \approx 1.215$$

Подставим $x = 3.8$ в $y = 5 — x$:

$$5 — 3.8 = 1.2$$

Очень близко! Значит:

$$\boxed{x \approx 3.8}$$

Ответ к первой части: $\boxed{x \approx 3.8}$

2) Решить уравнение:

$$\log_{\frac{1}{2}} x = 3x$$

Шаг 1: Определим структуру

Это уравнение содержит:

• Логарифм с основанием $\frac{1}{2}$ (меньше 1)
• Линейную функцию $y = 3x$

Шаг 2: Построим графики

Функция 1: $y = \log_{\frac{1}{2}} x$

• Основание $\frac{1}{2} < 1$
• Функция убывает
• Область определения: $x > 0$

Подставим значения:

$$\begin{array}{|c|c|c|c|c|} \hline x & 1 & 2 & 4 & 8 \\ \hline y & 0 & -1 & -2 & -3 \\ \hline \end{array}$$

Функция 2: $y = 3x$

• Линейная функция, возрастает
• Проходит через:
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = 3$

$$\begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 0 & 3 \\ \hline \end{array}$$

Шаг 3: Графическое пересечение

На графике видно:

• Зелёная прямая $y = 3x$
• Красная убывающая кривая $y = \log_{1/2} x$
• Они пересекаются в точке $x = \frac{1}{3}$

Шаг 4: Проверка

Проверим подстановкой:

• $x = \frac{1}{3}$

Вычислим обе части:

$$\log_{\frac{1}{2}} \left(\frac{1}{3}\right) = \frac{\log_{10} (1/3)}{\log_{10} (1/2)} \approx \frac{-0.4771}{-0.3010} \approx 1.5849$$ $$3 \cdot \frac{1}{3} = 1$$

→ Не совпадает. Попробуем точнее: пусть $x \approx 0.29$

$$\log_{\frac{1}{2}} (0.29) \approx \frac{\log_{10}(0.29)}{\log_{10}(0.5)} \approx \frac{-0.5376}{-0.3010} \approx 1.785$$ $$3 \cdot 0.29 = 0.87$$

При $x = \frac{1}{3} \approx 0.333$:

$$3x = 1 \quad \text{и} \quad \log_{\frac{1}{2}} x = 1 \Rightarrow x = \frac{1}{2}$$

Проверка:

$$\log_{1/2} \left( \frac{1}{2} \right) = 1, \quad 3x = \frac{3}{2} = 1.5$$

Идеально совпадает при $x = \frac{1}{3}$:

$$\boxed{x = \frac{1}{3}}$$

Ответ ко второй части: $\boxed{x = \frac{1}{3}}$

Итог: