ГДЗ по Алгебре 10-11 Класс Номер 374 Алимов — Подробные Ответы

Построить график функции:

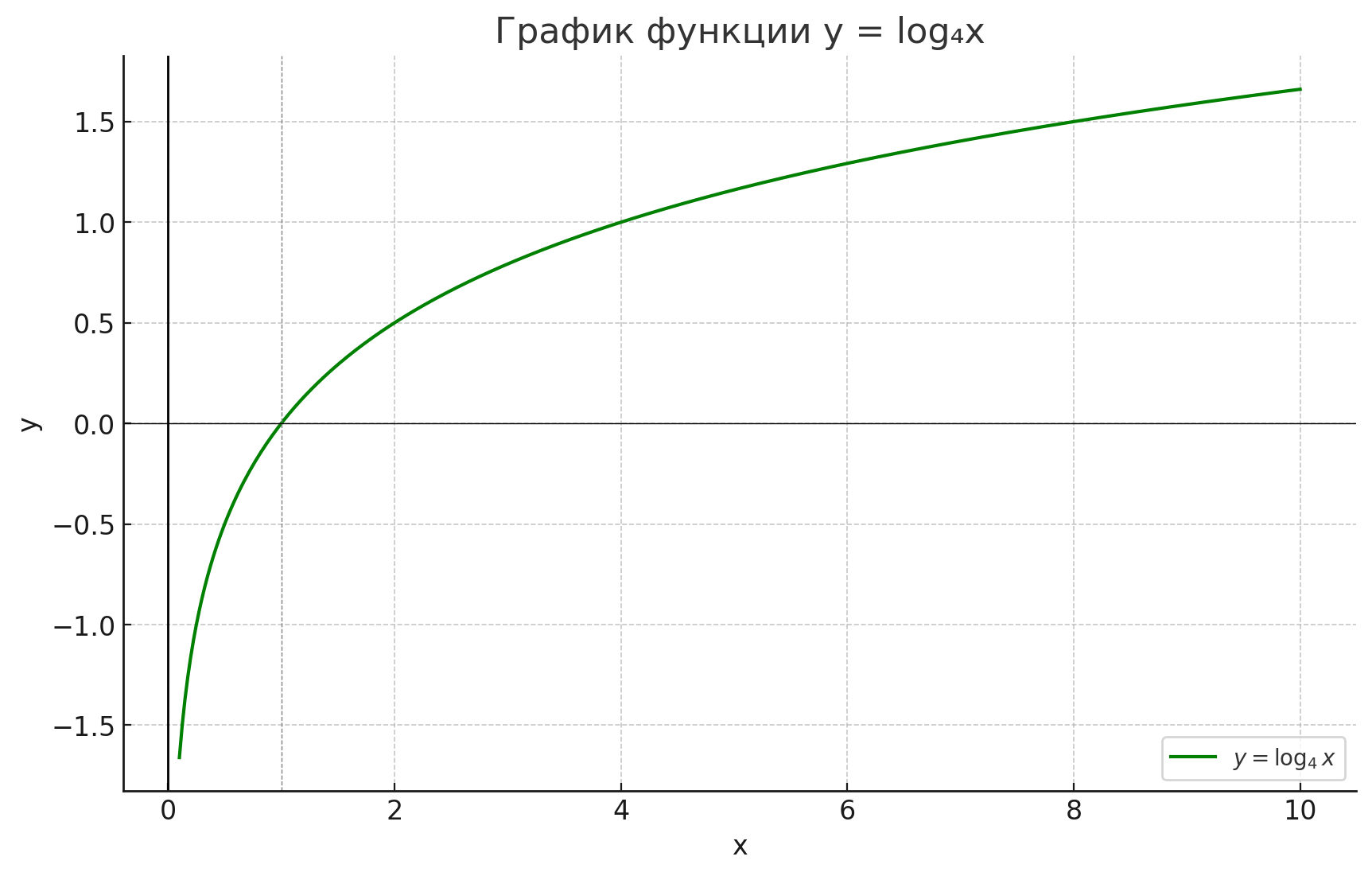
1. у = log4(х);
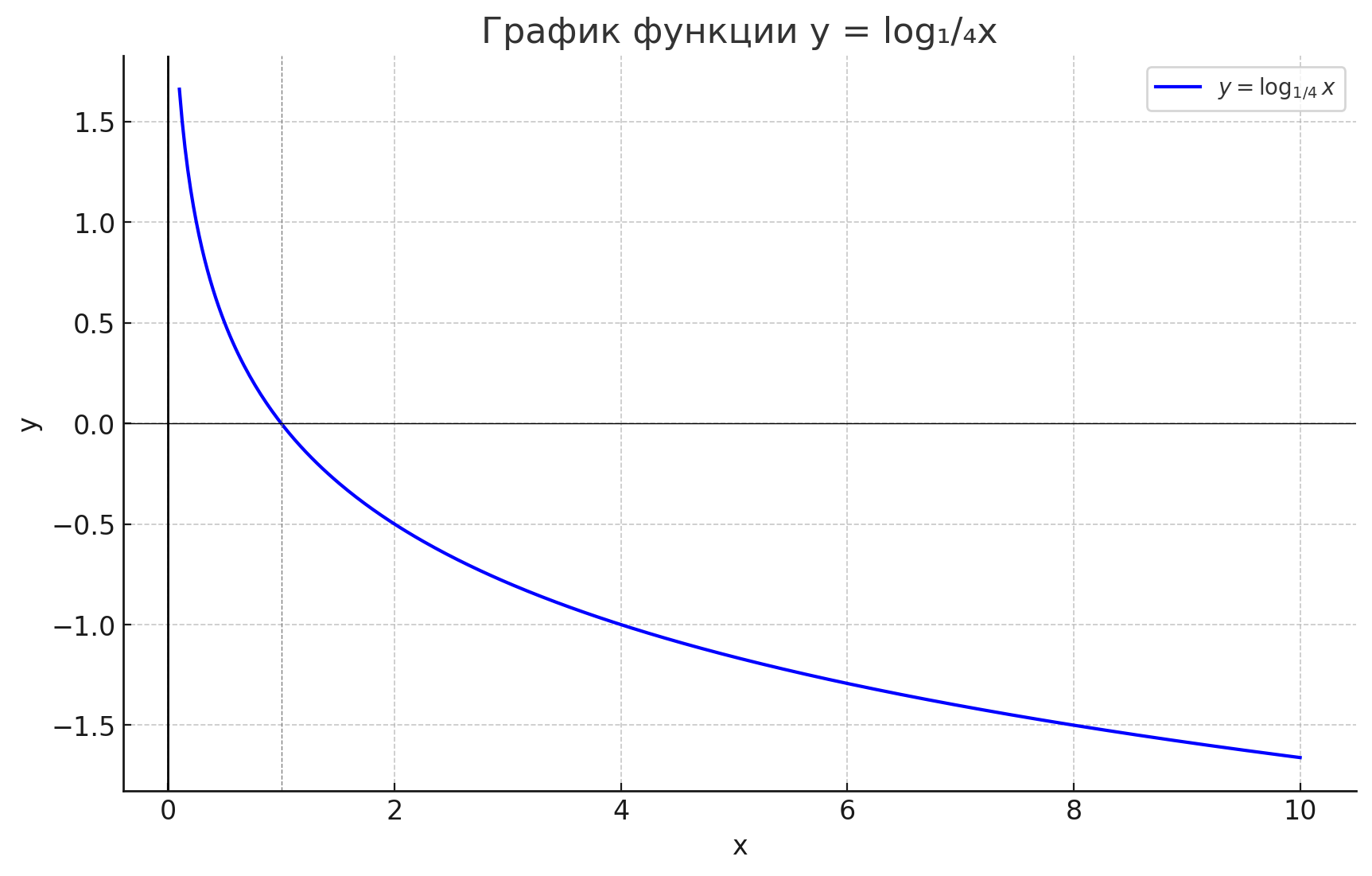
2. у = log1/4(х).

Какая из данных функций является возрастающей? убывающей? При каких значениях х каждая функция принимает положительные значения? отрицательные значения? значения, равные нулю?

$y = \log_4 x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция возрастает, так как: $4 > 1$;
• Функция равна нулю при: $x = 1$;
• Функция положительна при: $x > 1$;
• Функция отрицательна при: $0 < x < 1$;

Координаты некоторых точек:

$$\begin{array}{|c|c|c|c|} \hline x & 1 & 4 & 16 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

График функции:

$y = \log_{\frac{1}{4}} x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция убывает, так как: $0 < \frac{1}{4} < 1$;
• Функция равна нулю при: $x = 1$;
• Функция положительна при: $0 < x < 1$;
• Функция отрицательна при: $x > 1$;

Координаты некоторых точек:

$$\begin{array}{|c|c|c|c|} \hline x & 1 & 4 & 16 \\ \hline y & 0 & -1 & -2 \\ \hline \end{array}$$

График функции:

1) Функция: $y = \log_4 x$

Шаг 1: Определение логарифма

Функция $y = \log_4 x$ означает:

«Найти такое число $y$, при котором основание логарифма $4$, возведённое в степень $y$, даёт число $x$«.

То есть:

$$\log_4 x = y \iff 4^y = x$$

Шаг 2: Область определения

Формально:

$$x > 0$$

Почему? Логарифм определён только для положительных чисел. Нельзя взять логарифм от 0 или отрицательного числа по определению.

Шаг 3: Множество значений

$$y \in \mathbb{R}$$

Почему? Логарифм может принимать любые действительные значения: от $-\infty$ до $+\infty$. Например:

• $\log_4 1 = 0$
• $\log_4 4 = 1$
• $\log_4 16 = 2$
• $\log_4 \tfrac{1}{4} = -1$

Шаг 4: Поведение функции

• Основание $a = 4 > 1$
  Значит, функция возрастает. То есть, чем больше $x$, тем больше $y$.

График идёт снизу вверх.

Шаг 5: Нули функции

$$\log_4 x = 0 \iff 4^0 = 1 \Rightarrow x = 1$$

То есть график пересекает ось X в точке (1, 0).

Шаг 6: Знак функции

• Положительная:

  $$\log_4 x > 0 \iff x > 1$$

• Отрицательная:

  $$\log_4 x < 0 \iff 0 < x < 1$$

Шаг 7: Таблица значений

Построим табличку вручную:

Пояснение:

• $\log_4 1 = 0$ потому что $4^0 = 1$
• $\log_4 4 = 1$ потому что $4^1 = 4$
• $\log_4 16 = 2$ потому что $4^2 = 16$

Шаг 8: График

• График проходит через:
  • (1, 0)
  • (4, 1)
  • (16, 2)
• При $x \to 0^+$, $y \to -\infty$
• При $x \to \infty$, $y \to \infty$

Форма: медленно растущая кривая, идущая снизу вверх справа.

2) Функция: $y = \log_{\frac{1}{4}} x$

Шаг 1: Логарифм с основанием меньше 1

Основание $\frac{1}{4} < 1$, но всё ещё положительное. Логарифм корректен.

$$\log_{\frac{1}{4}} x = y \iff \left(\frac{1}{4}\right)^y = x$$

Шаг 2: Область определения

Как и раньше:

$$x > 0$$

Шаг 3: Множество значений

$$y \in \mathbb{R}$$

Всё аналогично первому случаю.

Шаг 4: Поведение функции

• $0 < \frac{1}{4} < 1$
• Это означает, что функция убывает: чем больше $x$, тем меньше $y$

График идёт сверху вниз.

Шаг 5: Нули функции

$$\log_{\frac{1}{4}} x = 0 \Rightarrow \left(\frac{1}{4}\right)^0 = 1 \Rightarrow x = 1$$

Так же как и раньше: точка (1, 0)

Шаг 6: Знак функции

• Положительная:

  $$\log_{\frac{1}{4}} x > 0 \iff 0 < x < 1$$

• Отрицательная:

  $$\log_{\frac{1}{4}} x < 0 \iff x > 1$$

Функция «зеркальна» по отношению к функции $\log_4 x$ — по оси X.

Шаг 7: Таблица значений

Пояснение:

• $\left(\frac{1}{4}\right)^0 = 1$
• $\left(\frac{1}{4}\right)^{-1} = 4$
• $\left(\frac{1}{4}\right)^{-2} = 16$

Шаг 8: График

• Проходит через:
  • (1, 0)
  • (4, -1)
  • (16, -2)
• При $x \to 0^+$, $y \to \infty$
• При $x \to \infty$, $y \to -\infty$

Форма: медленно убывающая кривая, идущая сверху вниз.

Итоговое сравнение графиков