ГДЗ по Алгебре 10-11 Класс Номер 324 Алимов — Подробные Ответы

Изобразить схематически график функции:

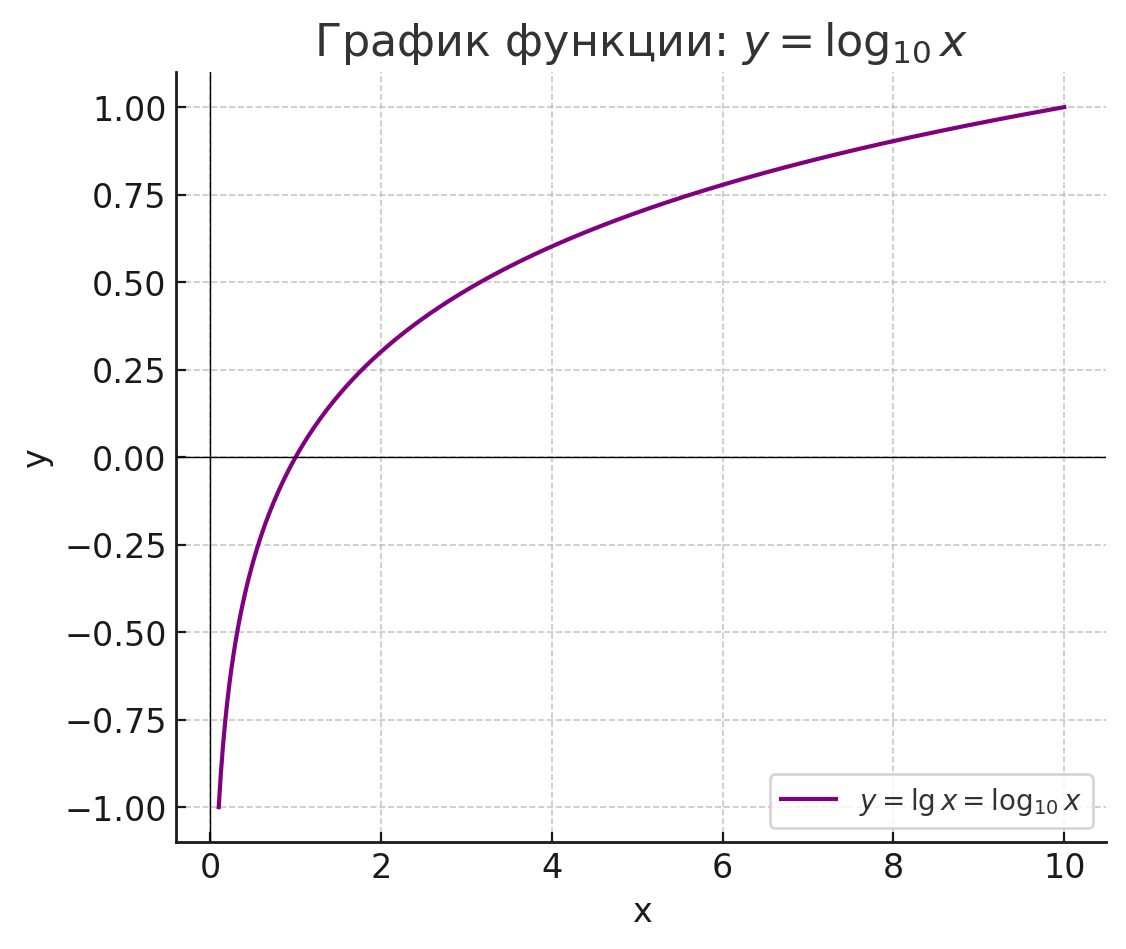
1. y=lgx;
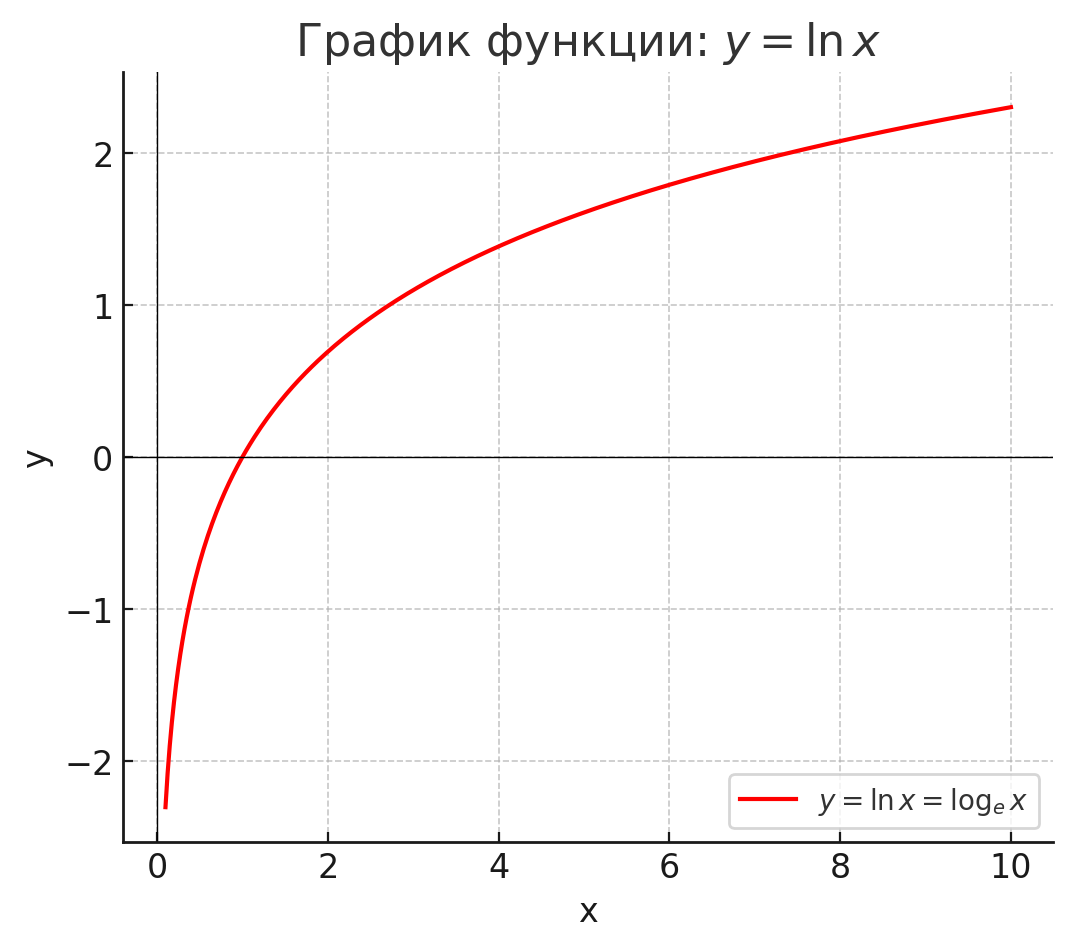
2. у = lnх;
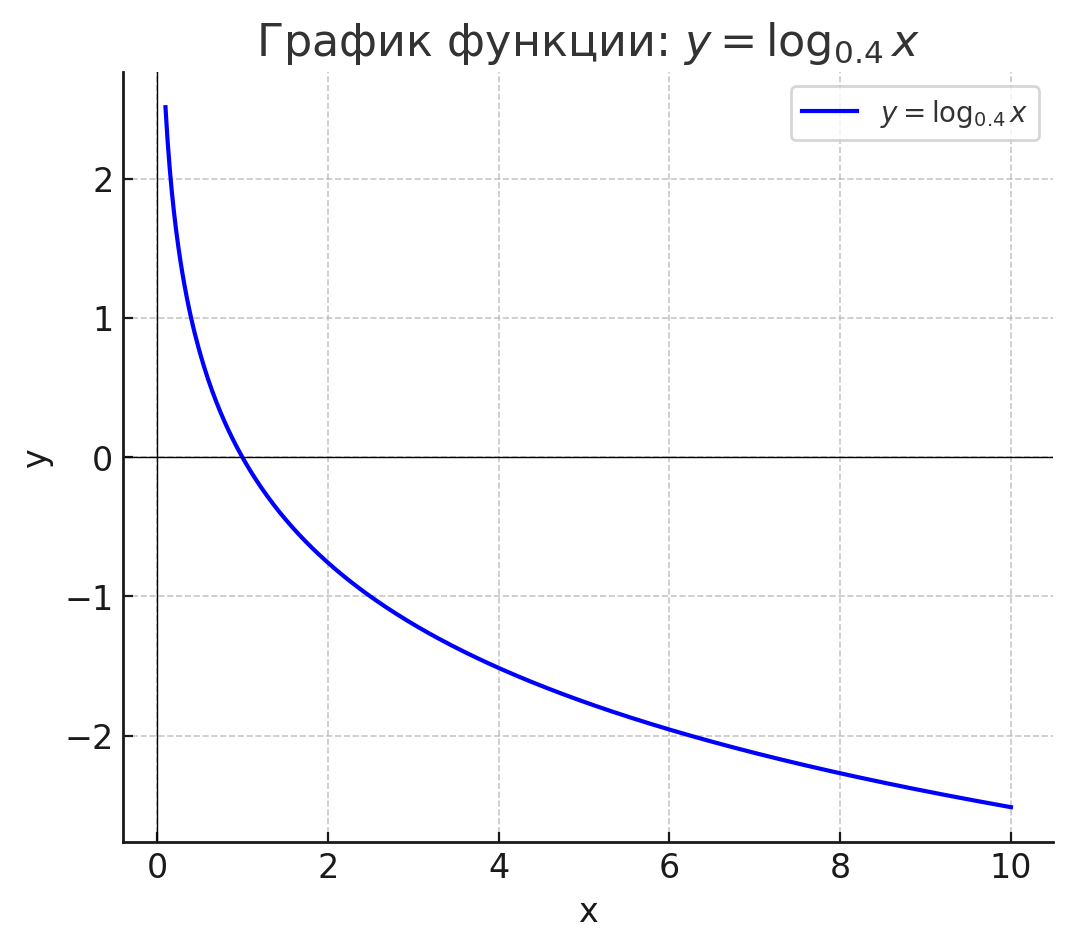
3. y = log0,4(x);
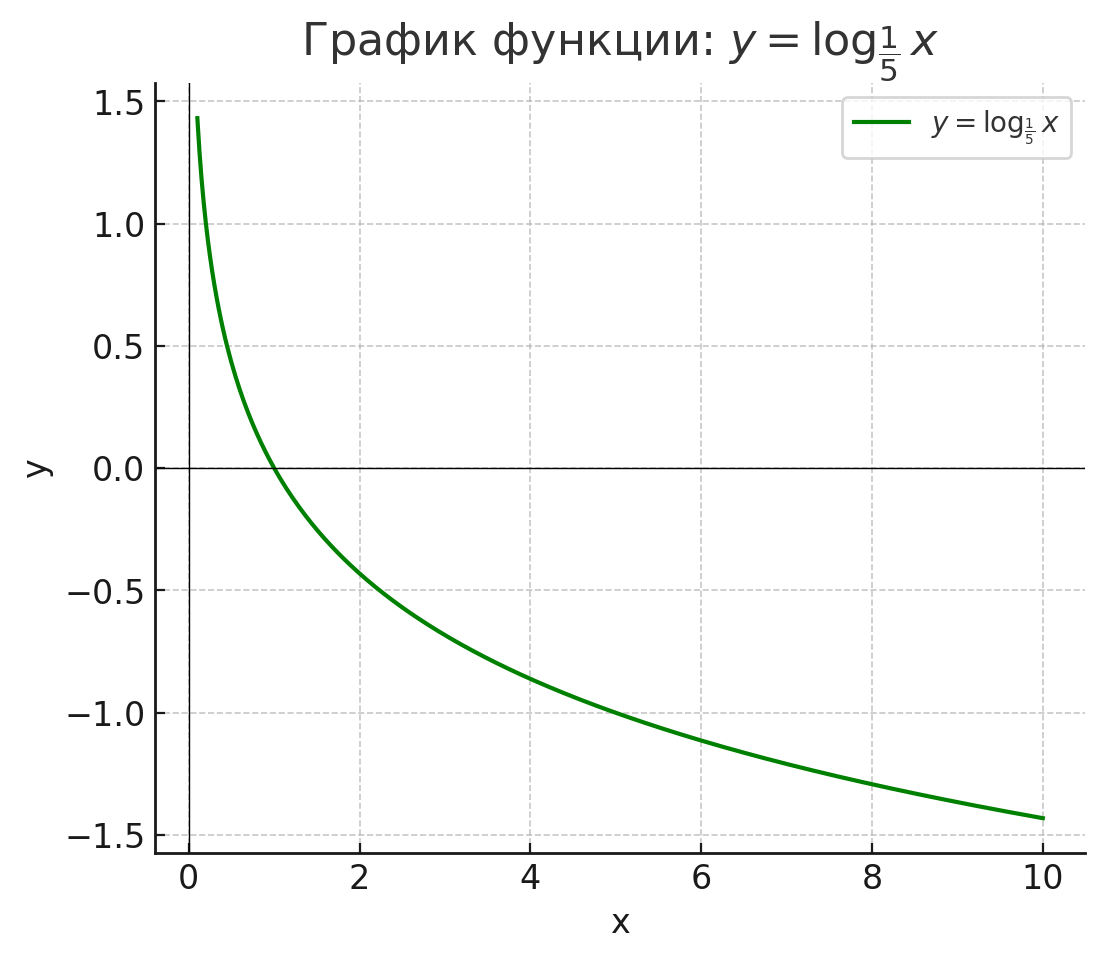
4. y=log1/5(x).

1) $y = \lg x = \log_{10} x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция возрастает, так как $10 > 1$;

Схематичный график функции:

2) $y = \ln x = \log_{e} x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция возрастает, так как $e > 1$;

Схематичный график функции:

3) $y = \log_{0.4} x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция убывает, так как $0 < 0.4 < 1$;

Схематичный график функции:

4) $y = \log_{\frac{1}{5}} x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция убывает, так как $0 < \frac{1}{5} < 1$;

Схематичный график функции:

1) $y = \lg x = \log_{10} x$

Область определения:

Логарифм существует только при положительном аргументе:

$$\boxed{x > 0}$$

Множество значений:

Значения логарифма могут быть любым действительным числом:

$$\boxed{y \in \mathbb{R}}$$

Поведение функции:

Основание логарифма $10 > 1$, значит:

$$\boxed{\text{Функция возрастает}}$$

Примеры точек:

• $\log_{10} 1 = 0$
• $\log_{10} 10 = 1$
• $\log_{10} 100 = 2$

График:

Функция возрастает, проходит через точку (1; 0), плавно поднимается вправо.
Слева стремится к $-\infty$ при $x \to 0^+$, но никогда не касается оси Oy.

2) $y = \ln x = \log_e x$

Область определения:

$$\boxed{x > 0}$$

Множество значений:

$$\boxed{y \in \mathbb{R}}$$

Поведение функции:

Поскольку $e \approx 2{,}718 > 1$:

$$\boxed{\text{Функция возрастает}}$$

Примеры точек:

• $\ln 1 = 0$
• $\ln e = 1$
• $\ln e^2 = 2$

График:

Очень похож на $\log_{10} x$, но растёт чуть быстрее.
Проходит через (1; 0) и (e; 1).
Также стремится к $-\infty$ при $x \to 0^+$.

3) $y = \log_{0.4} x$

Область определения:

$$\boxed{x > 0}$$

Множество значений:

$$\boxed{y \in \mathbb{R}}$$

Поведение функции:

Основание $a = 0.4$, и так как:

$$0 < 0.4 < 1 \Rightarrow \boxed{\text{Функция убывает}}$$

Примеры точек:

• $\log_{0.4} 1 = 0$
• $\log_{0.4} 0.4 = 1$
• $\log_{0.4} 0.16 = 2$
  (так как $0.4^2 = 0.16$)

График:

Функция убывает, идёт сверху вниз.
Проходит через (1; 0).
При $x \to 0^+$, $y \to +\infty$,
при $x \to +\infty$, $y \to -\infty$.

4) $y = \log_{\frac{1}{5}} x$

Область определения:

$$\boxed{x > 0}$$

Множество значений:

$$\boxed{y \in \mathbb{R}}$$

Поведение функции:

$$0 < \frac{1}{5} < 1 \Rightarrow \boxed{\text{Функция убывает}}$$

Примеры точек:

• $\log_{1/5} 1 = 0$
• $\log_{1/5} \frac{1}{5} = 1$
• $\log_{1/5} \left(\frac{1}{25}\right) = 2$
  (так как $\left(\frac{1}{5}\right)^2 = \frac{1}{25}$)

График:

Очень похож на график $\log_{0.4} x$, но убывает резче, так как основание ближе к 0.
Идёт сверху вниз, справа налево, с теми же пределами.

Вывод: