ГДЗ по Алгебре 10-11 Класс Номер 323 Алимов — Подробные Ответы

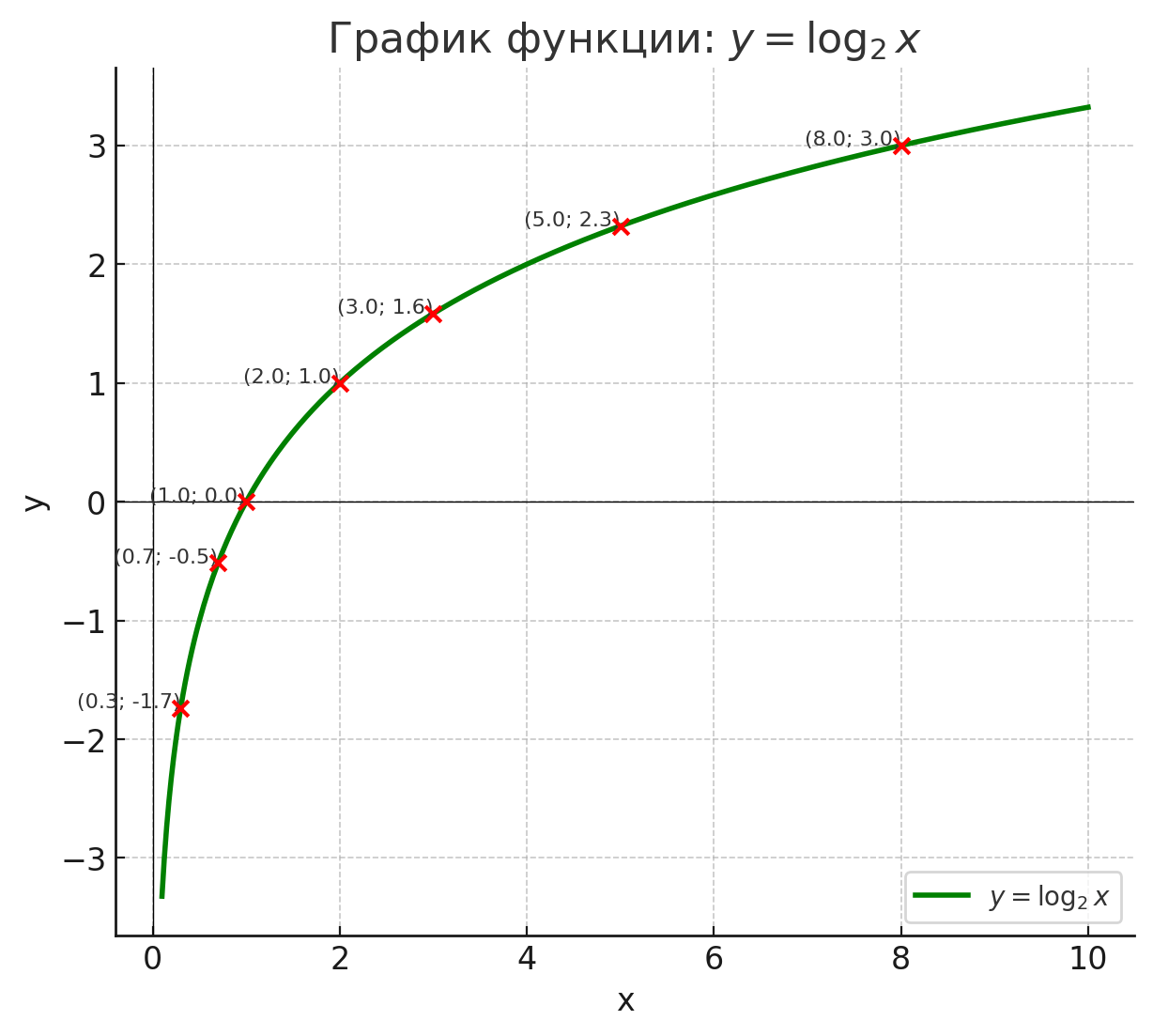
По графику функции у = log2(х) найти приближённо log2(3), log2(0,3), log2(5), log2(0,7).

Дана функция: $y = \log_{2} x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция возрастает, так как $2 > 1$;

Координаты некоторых точек:

График функции:

Найдем приближенные значения чисел:

1. $\log_{2} 3 \approx 1.6$;
2. $\log_{2} 0.3 \approx -1.7$;
3. $\log_{2} 5 \approx 2.3$;
4. $\log_{2} 0.7 \approx -0.5$;

Дана функция:

$$y = \log_{2} x$$

ШАГ 1: Область определения

Функция логарифма определена только для положительных значений переменной $x$:

$$x > 0$$

Это означает, что в графике и вычислениях нельзя использовать отрицательные значения или ноль.

$$\boxed{\text{Область определения: } x > 0}$$

ШАГ 2: Множество значений

Логарифмическая функция может принимать любое действительное значение $y$. Это означает:

• При больших $x$ — $y \to +\infty$
• При $x \to 0^+$ — $y \to -\infty$

$$\boxed{\text{Множество значений: } y \in \mathbb{R}}$$

ШАГ 3: Возрастание функции

Функция $y = \log_a x$ возрастает, если $a > 1$.

В нашем случае основание:

$$a = 2 > 1 \Rightarrow \boxed{\text{Функция возрастает}}$$

Это значит: чем больше значение $x$, тем больше значение $y$.

ШАГ 4: Точные значения функции в отдельных точках

Подставим конкретные значения:

$$\boxed{ \text{Координаты: } (1;0), (2;1), (8;3) }$$

ШАГ 5: Приближённые значения логарифмов

Посчитаем значения, которые не выражаются целым числом:

1. $\log_2 3 \approx 1.6$
   (так как $2^1 = 2$, $2^2 = 4$, значит $\log_2 3$ между 1 и 2)
2. $\log_2 0.3 \approx -1.7$
   (значение меньше 1, логарифм отрицателен; ближе к 0)
3. $\log_2 5 \approx 2.3$
   (так как $2^2 = 4$, $2^3 = 8$; 5 между ними)
4. $\log_2 0.7 \approx -0.5$
   (так как $2^{-1} = 0.5$, $2^0 = 1$; 0.7 между ними)

ШАГ 6: График функции

Форма графика:

• Проходит через точку (1, 0) — любая логарифмическая функция проходит через неё.
• Ветвь графика идёт от левой стороны (приближаясь к оси $Oy$, но не касаясь её) вверх вправо.
• Чем больше $x$, тем больше $y$.
• При $x \to 0^+$, $y \to -\infty$.

Графическое изображение

ИТОГОВЫЙ ВЫВОД:

• Область определения: $x > 0$
• Множество значений: $y \in \mathbb{R}$
• Функция возрастает
• Точные значения:
  $\log_2 1 = 0$,
  $\log_2 2 = 1$,
  $\log_2 8 = 3$
• Приближённые значения:
  $\log_2 3 \approx 1.6$,
  $\log_2 0.3 \approx -1.7$,
  $\log_2 5 \approx 2.3$,
  $\log_2 0.7 \approx -0.5$