ГДЗ по Алгебре 10-11 Класс Номер 322 Алимов — Подробные Ответы

Построить график функции:

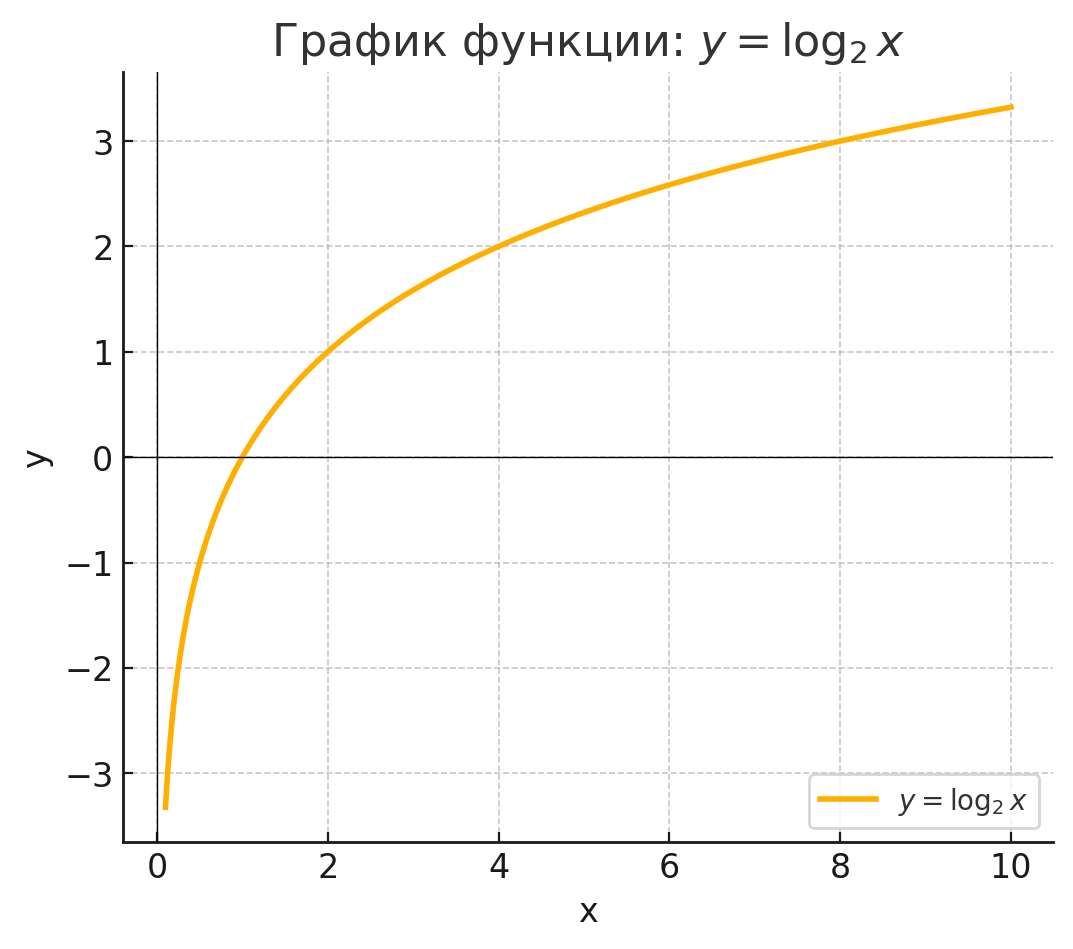
1. y=log2(x);
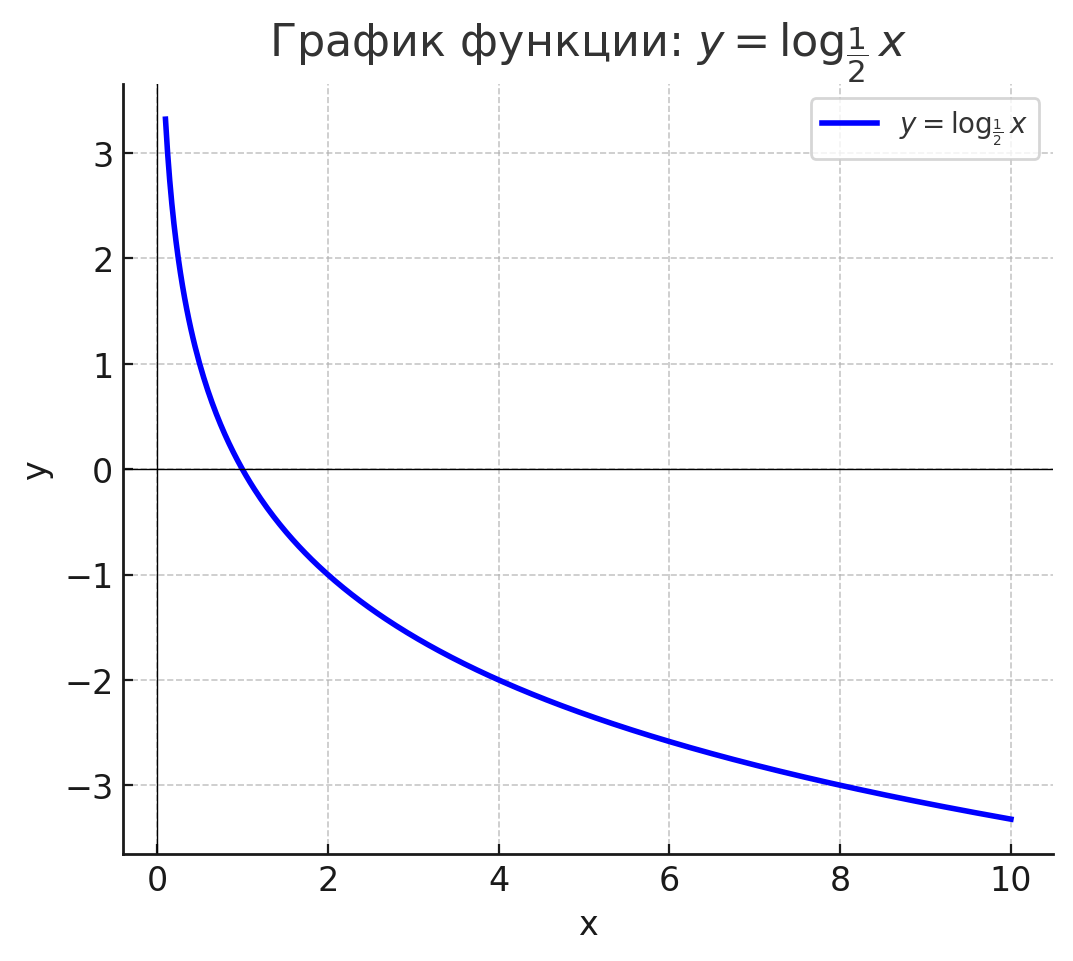
2. y= log1/2(x).

1) $y = \log_{2} x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция возрастает, так как $2 > 1$;

Координаты некоторых точек:

График функции:

2) $y = \log_{\frac{1}{2}} x$

• Область определения: $x > 0$;
• Множество значений: $y \in \mathbb{R}$;
• Функция убывает, так как $0 < \frac{1}{2} < 1$;

Координаты некоторых точек:

График функции:

$$\boxed{ \text{Текст изображен в соответствии с заданием.} }$$

1) $y = \log_{2} x$

ШАГ 1: Определим область определения

Функция $y = \log_{2} x$ определена только при положительных значениях переменной $x$, поскольку логарифм существует только для положительных аргументов.

$$\boxed{x > 0}$$

ШАГ 2: Найдём множество значений

Логарифмическая функция с любым допустимым основанием (кроме 1) принимает все действительные значения — то есть может быть как положительной, так и отрицательной, и равной нулю.

$$\boxed{y \in \mathbb{R}}$$

ШАГ 3: Исследуем поведение функции (возрастает/убывает)

Для этого смотрим на основание логарифма:

$$a = 2$$

Так как:

• $a > 1$,
• логарифмическая функция возрастает: при увеличении $x$, значение $y = \log_{2} x$ увеличивается.

$$\boxed{\text{Функция возрастает}}$$

ШАГ 4: Подставим конкретные значения $x$, чтобы найти точки

$$\boxed{ \text{Координаты точек: } (1; 0), (2; 1), (8; 3) }$$

ШАГ 5: График

График функции проходит через эти точки, асимптотически приближается к оси $Oy$ слева, и возрастает вправо. Он расположен только в правой части координатной плоскости, так как $x > 0$.

2) $y = \log_{\frac{1}{2}} x$

ШАГ 1: Область определения

Как и в предыдущем случае: логарифм определён только при $x > 0$.

$$\boxed{x > 0}$$

ШАГ 2: Множество значений

Любая логарифмическая функция, даже с основанием $a < 1$, имеет все действительные значения.

$$\boxed{y \in \mathbb{R}}$$

ШАГ 3: Исследуем поведение функции

Здесь основание:

$$a = \frac{1}{2}$$

Так как:

• $0 < \frac{1}{2} < 1$,
• функция убывает: при увеличении $x$, значение $y$ уменьшается.

$$\boxed{\text{Функция убывает}}$$

ШАГ 4: Найдём конкретные точки

Почему такие значения?
Потому что:

• $\left(\frac{1}{2}\right)^{-1} = 2$
• $\left(\frac{1}{2}\right)^{-3} = 8$

ШАГ 5: График

График функции убывает, находится в правой полуплоскости, и также асимптотически приближается к оси $Oy$ слева. Убывает, потому что основание меньше единицы.

Ответ:

$$\boxed{ \text{Функция } y = \log_{2} x \text{ возрастает, } y = \log_{\frac{1}{2}} x \text{ убывает.} }$$