
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 254 Алимов — Подробные Ответы
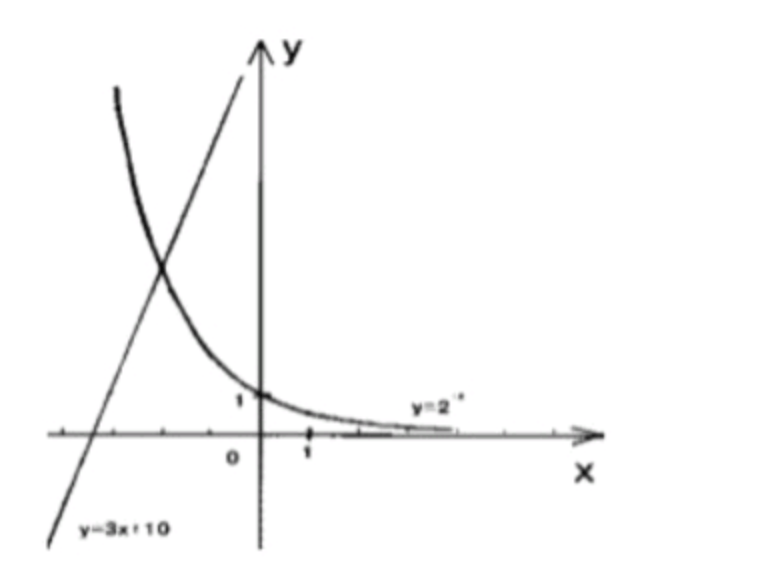
- 2^-x =3x+10;
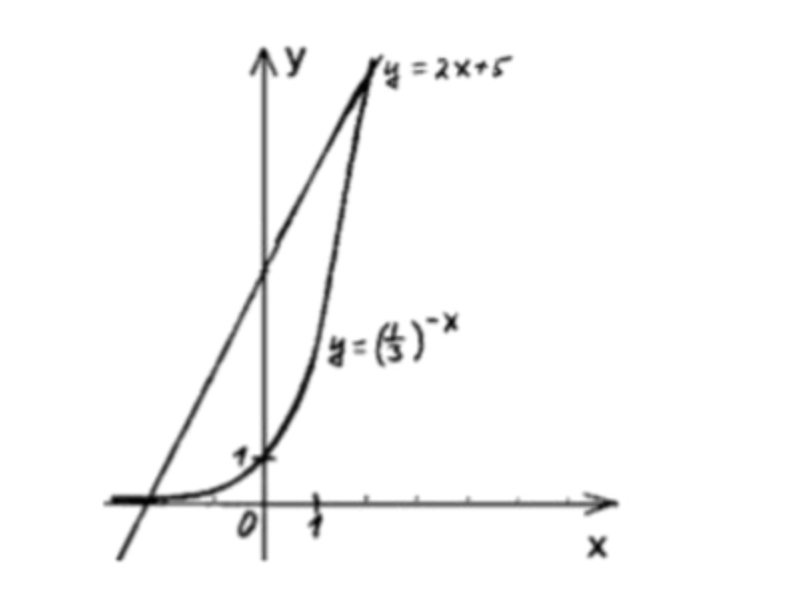
- (1/3)^-x = 2x+5.
1)
— показательная функция:
— уравнение прямой:
Ответ: .
2)
— показательная функция:
— уравнение прямой:
Ответ: .
Задача 1
Уравнение:
Шаг 1: Разберём, что нам даны за функции
У нас есть две функции:
— показательная функция, где основание больше 1, значит, эта функция будет убывающей. Для некоторых значений мы уже имеем значения :
Это значит, что при , при , а при .
— это линейная функция, у которой:
Этот график является прямой с угловым коэффициентом 3 и с пересечением с осью на уровне .
Шаг 2: Построение графиков
Чтобы найти решение, давай рассмотрим графики обеих функций.
График будет убывающим, так как основание степени больше 1.
График — прямая линия, с угловым коэффициентом 3 и пересечением с осью на .
Тогда мы ищем точку пересечения этих двух графиков, то есть значение , при котором .
Шаг 3: Приближённый поиск решения
Мы видим, что при значение , а при значение , в то время как правая часть уравнения при даёт 1, а при даёт 4.
Следовательно, решение уравнения должно быть между и . Из графика мы видим, что точка пересечения примерно находится в .
Ответ: .
Задача 2
Уравнение:
Шаг 1: Разберём, что нам даны за функции
— это также показательная функция, но с основанием , которое меньше 1. Это означает, что эта функция будет возрастающей. Для некоторых значений нам даны значения :
То есть при , при , при .
— это линейная функция. Для этой функции у нас есть следующие значения:
График этой функции — прямая, которая растёт с угловым коэффициентом 3.
Шаг 2: Построение графиков
Мы ищем точку пересечения графиков и .
- График — это возрастающая показательная функция.
- График — это линейная функция, растущая с угловым коэффициентом 3.
Шаг 3: Приближённый поиск решения
Для приближённого нахождения точек пересечения мы можем оценить, что:
- При , , а .
- При , , а .
- При , , а .
Таким образом, одна из точек пересечения, очевидно, находится между и , а вторая — при .
Ответ: , .



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!