ГДЗ по Алгебре 10-11 Класс Учебник 📕 Алимов — Все Части

Алгебра

10-11 класс учебник Алимов

10 класс

Тип

ГДЗ, Решебник.

Автор

Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.

Год

2015-2024.

Издательство

Просвещение.

Описание

Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.

Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.

Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.

Преимущества учебника

Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения.
Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач.
Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам.
Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры.
Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.

Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.

ГДЗ по Алгебре 10-11 Класс Номер 200 Алимов — Подробные Ответы

Задача

Решить графически неравенство:

(1/3)x > 1;
(1/20)x < 1;
5x > 5;
5x > 1/5.

Краткий ответ:

1) $\left(\frac{1}{3}\right)^x > 1$ ;

Рассмотрим функцию $y = \left(\frac{1}{3}\right)^x$ :

Область определения: $x \in R$ ;
Множество значений: $y > 0$ ;
Функция убывает, так как $0 < \frac{1}{3} < 1$ ;

$x$	$-2$	$-1$	$0$
$y$	$9$	$3$	$1$

$x$

$-2$

$-1$

$0$

$y$

$9$

$3$

$1$

График функции:

Ответ: $x < 0$

2) $\left(\frac{1}{2}\right)^x < 1$ ;

Рассмотрим функцию $y = \left(\frac{1}{2}\right)^x$ :

Область определения: $x \in R$ ;
Множество значений: $y > 0$ ;
Функция убывает, так как $0 < \frac{1}{2} < 1$ ;

$x$	$-2$	$-1$	$0$
$y$	$4$	$2$	$1$

$x$

$-2$

$-1$

$0$

$y$

$4$

$2$

$1$

График функции:

Ответ: $x > 0$

3) $5^x > 5$ ;

Рассмотрим функцию $y = 5^x$ :

Область определения: $x \in R$ ;
Множество значений: $y > 0$ ;
Функция возрастает, так как $5 > 1$ ;

$x$	$0$	$1$	$2$
$y$	$1$	$5$	$25$

$x$

$0$

$1$

$2$

$y$

$1$

$5$

$25$

График функции:

Ответ: $x > 1$

4) $5^x < \frac{1}{5}$ ;

Рассмотрим функцию $y = 5^x$ :

Область определения: $x \in R$ ;

Множество значений: $y > 0$ ;

Функция возрастает, так как $5 > 1$ ;

$x$	$-1$	$0$	$1$
$y$	$0.2$	$1$	$5$

$x$

$-1$

$0$

$1$

$y$

$0.2$

$1$

$5$

График функции:

Ответ: $x < -1$

Подробный ответ:

1) $\left(\frac{1}{3}\right)^x > 1$ ;

Рассмотрим функцию $y = \left(\frac{1}{3}\right)^x$ :

Область определения:

Функция определена для всех значений x, так как основание $\frac{1}{3}$ положительно и не равно нулю.
Следовательно, область определения: $x \in R$ .

Множество значений:

Поскольку $\frac{1}{3} > 0$ , функция всегда принимает положительные значения $y > 0$ .

Анализ монотонности:

Основание $\frac{1}{3}$ $y = {(\frac{1}{3})}^{x}$
При увеличении x, значения функции будут уменьшаться. То есть, если $x_1 < x_2$ , то $\left(\frac{1}{3}\right)^{x_1} > \left(\frac{1}{3}\right)^{x_2}$ .

Построение таблицы значений: Рассмотрим некоторые значения функции для $x = -2, -1, 0$ :

$x$	$-2$	$-1$	$0$
$y$	$9$	$3$	$1$

$x$

$-2$

$-1$

$0$

$y$

$9$

$3$

$1$

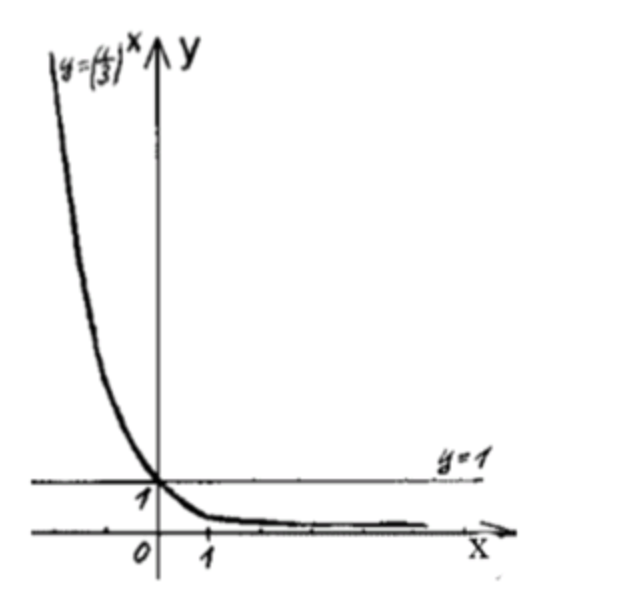
График функции будет убывать: начиная от значения 9 при $x = -2$ , и плавно переходя через 3 и 1 до $x = 0$ .

Решение неравенства: Мы ищем, при каких значениях $x$ выполняется неравенство $\left(\frac{1}{3}\right)^x > 1$ .

Для того, чтобы ${(\frac{1}{3})}^{x} > 1$ , $x$ должно быть отрицательным, так как функция убывает, и для отрицательных значений $x$ функция принимает значения больше 1.

Ответ: $x < 0$ $x < 0$

2) $\left(\frac{1}{2}\right)^x < 1$ ;

Рассмотрим функцию $y = \left(\frac{1}{2}\right)^x$ :

Область определения:

Функция определена для всех значений x, так как основание $\frac{1}{2}$ положительно и не равно нулю.
Следовательно, область определения: $x \in R$ .

Множество значений:

Поскольку $\frac{1}{2} > 0$ , функция всегда принимает положительные значения $y > 0$ .

Анализ монотонности:

Основание $\frac{1}{2}$ $y = {(\frac{1}{2})}^{x}$
При увеличении x, значения функции будут уменьшаться.

Построение таблицы значений: Рассмотрим некоторые значения функции для $x = -2, -1, 0$ :

$x$	$-2$	$-1$	$0$
$y$	$4$	$2$	$1$

$x$

$-2$

$-1$

$0$

$y$

$4$

$2$

$1$

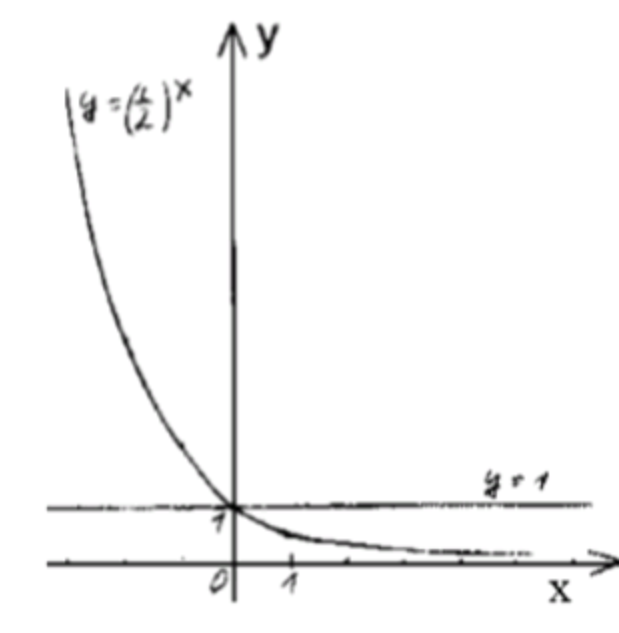
График функции будет убывать: начиная от значения 4 при $x = -2$ , и плавно переходя через 2 и 1 до $x = 0$ .

Решение неравенства: Мы ищем, при каких значениях $x$ выполняется неравенство $\left(\frac{1}{2}\right)^x < 1$ .

Для того, чтобы ${(\frac{1}{2})}^{x} < 1$ , $x$ должно быть положительным, так как функция убывает, и для положительных значений $x$ функция будет меньше 1.

Ответ: $x > 0$

3) $5^x > 5$ ;

Рассмотрим функцию $y = 5^x$ :

Область определения:

Функция определена для всех значений x, так как основание 5 положительно и не равно нулю.
Следовательно, область определения: $x \in R$ .

Множество значений:

Поскольку $5 > 0$ , функция всегда принимает положительные значения $y > 0$ .

Анализ монотонности:

Основание $5 > 1$ , что означает, что функция $y = 5^x$ является возрастающей.
При увеличении x, значения функции будут увеличиваться.

Построение таблицы значений: Рассмотрим некоторые значения функции для $x = 0, 1, 2$ :

$x$	$0$	$1$	$2$
$y$	$1$	$5$	$25$

$x$

$0$

$1$

$2$

$y$

$1$

$5$

$25$

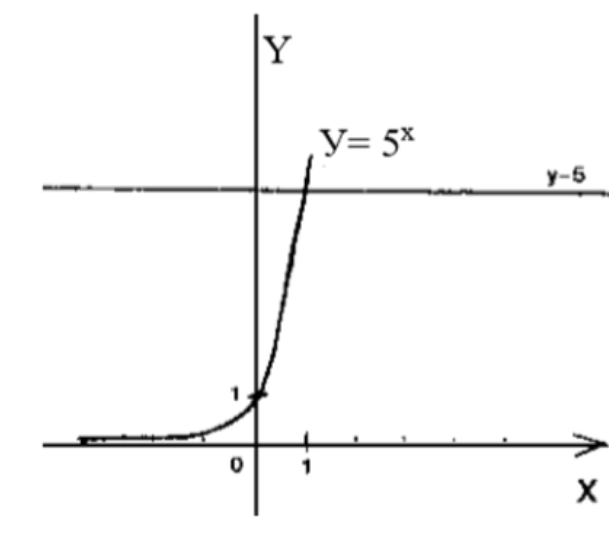
График функции будет возрастать: начиная от 1 при $x = 0$ , и плавно увеличиваясь до 25 при $x = 2$ .

Решение неравенства: Мы ищем, при каких значениях $x$ выполняется неравенство $5^x > 5$ .

Для того, чтобы $5^{x} > 5$ , $x$ должно быть больше 1, так как функция возрастает.

Ответ: $x > 1$ $x > 1$

4) $5^x < \frac{1}{5}$ ;

Рассмотрим функцию $y = 5^x$ :

Область определения:

Функция определена для всех значений x, так как основание 5 положительно и не равно нулю.
Следовательно, область определения: $x \in R$ .

Множество значений:

Поскольку $5 > 0$ , функция всегда принимает положительные значения $y > 0$ .

Анализ монотонности:

Основание $5 > 1$ , что означает, что функция $y = 5^x$ является возрастающей.
При увеличении x, значения функции будут увеличиваться.

Построение таблицы значений: Рассмотрим некоторые значения функции для $x = -1, 0, 1$ :

$x$	$-1$	$0$	$1$
$y$	$0.2$	$1$	$5$

$x$

$-1$

$0$

$1$

$y$

$0.2$

$1$

$5$

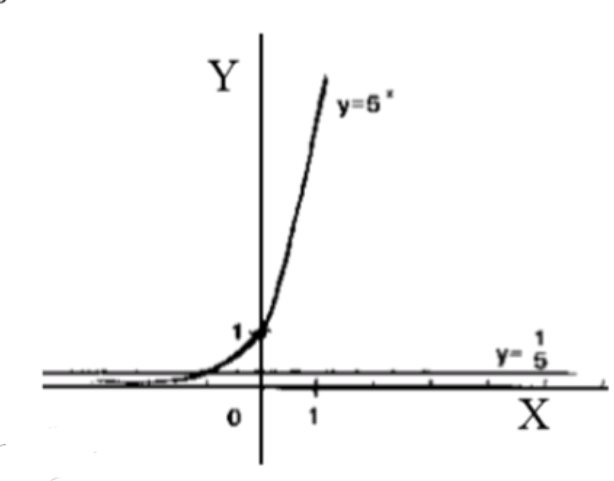
График функции будет возрастать: начиная от 0.2 при $x = -1$ , и плавно увеличиваясь до 5 при $x = 1$ .

Решение неравенства: Мы ищем, при каких значениях $x$ выполняется неравенство $5^x < \frac{1}{5}$ .

Для того, чтобы $5^{x} < \frac{1}{5}$ , $x$ должно быть меньше -1, так как функция возрастает.

Ответ: $x < - 1$

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Алгебра