ГДЗ по Алгебре 10-11 Класс Учебник 📕 Алимов — Все Части

Алгебра

10-11 класс учебник Алимов

10 класс

Тип

ГДЗ, Решебник.

Автор

Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.

Год

2015-2024.

Издательство

Просвещение.

Описание

Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.

Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.

Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.

Преимущества учебника

Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения.
Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач.
Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам.
Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры.
Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.

Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.

ГДЗ по Алгебре 10-11 Класс Номер 1158 Алимов — Подробные Ответы

Задача

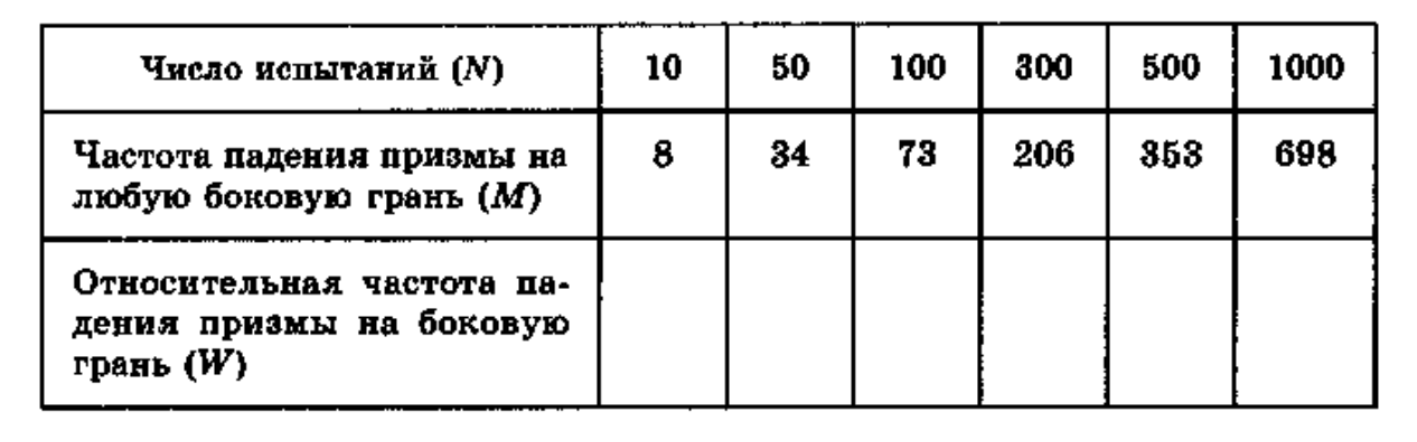
Проводились серии из N испытаний с подбрасыванием некоторой правильной треугольной призмы, сделанной из стали. Результаты заносились в таблицу:

Краткий ответ:

Заполним последнюю строку таблицы (с точностью до сотых):

Число испытаний (N)	10	50	100	300	500	1000
Частота падения призмы на любую боковую грань (M)	8	34	73	206	353	698
Относительная частота падения призмы на боковую грань (W)	0,80	0,68	0,73	0,69	0,71	0,70

$\begin{aligned} & W_{1} = \frac{M}{N} = \frac{8}{10} = 0,80; \\ & W_{2} = \frac{M}{N} = \frac{34}{50} = \frac{68}{100} = 0,68; \\ & W_{3} = \frac{M}{N} = \frac{73}{100} = 0,73; \\ & W_{4} = \frac{M}{N} = \frac{206}{300} = 0,68(6) \approx 0,69; \\ & W_{5} = \frac{M}{N} = \frac{353}{500} = 0,706 \approx 0,71; \\ & W_{6} = \frac{M}{N} = \frac{698}{1000} = 0,698 \approx 0,70; \end{aligned}$

По приведенной таблице очевидно, что частота (с точностью до одной десятой) события A — падение призмы на боковую грань, стремится к числу 0,7;

Ответ: P(A) = 0,7.

Подробный ответ:

Необходимо вычислить относительные частоты падения призмы на боковую грань для различных значений числа испытаний, используя данную таблицу.

В таблице для каждого числа испытаний $N$ дается количество успешных событий $M$ (падений призмы на боковую грань). Мы будем вычислять относительные частоты $W$ с точностью до сотых. Формула для вычисления относительной частоты:

$W = \frac{M}{N}$

где:

$M$ — количество успешных событий (в данном случае падений призмы на боковую грань),
$N$ — общее количество испытаний (то есть сколько раз выполнялось испытание).

Кроме того, в тексте задачи приведены также уже вычисленные частоты, которые нужно перепроверить и заново вывести с максимальной детализацией.

1. Вычисление относительной частоты для $N = 10$

Дано:
- $M = 8$ — количество успешных событий (падений призмы на боковую грань),
- $N = 10$ — количество испытаний.

Шаги вычисления:

Подставляем данные в формулу:
$W_1 = \frac{M}{N} = \frac{8}{10}$
Выполняем деление:
$W_1 = 0,80$
Ответ: относительная частота $W_1 = 0,80$ .

2. Вычисление относительной частоты для $N = 50$

Дано:
- $M = 34$ — количество успешных событий (падений призмы на боковую грань),
- $N = 50$ — количество испытаний.

Шаги вычисления:

Подставляем данные в формулу:
$W_2 = \frac{M}{N} = \frac{34}{50}$
Выполняем деление:
$W_2 = 0,68$
Ответ: относительная частота $W_2 = 0,68$ .

3. Вычисление относительной частоты для $N = 100$

Дано:
- $M = 73$ — количество успешных событий (падений призмы на боковую грань),
- $N = 100$ — количество испытаний.

Шаги вычисления:

Подставляем данные в формулу:
$W_3 = \frac{M}{N} = \frac{73}{100}$
Выполняем деление:
$W_3 = 0,73$
Ответ: относительная частота $W_3 = 0,73$ .

4. Вычисление относительной частоты для $N = 300$

Дано:
- $M = 206$ — количество успешных событий (падений призмы на боковую грань),
- $N = 300$ — количество испытаний.

Шаги вычисления:

Подставляем данные в формулу:
$W_4 = \frac{M}{N} = \frac{206}{300}$
Выполняем деление:
$W_4 = 0,6866\ldots$
Округляем результат до сотых:
$W_4 \approx 0,69$
Ответ: относительная частота $W_4 = 0,69$ .

5. Вычисление относительной частоты для $N = 500$

Дано:
- $M = 353$ — количество успешных событий (падений призмы на боковую грань),
- $N = 500$ — количество испытаний.

Шаги вычисления:

Подставляем данные в формулу:
$W_5 = \frac{M}{N} = \frac{353}{500}$
Выполняем деление:
$W_5 = 0,706$
Округляем результат до сотых:
$W_5 \approx 0,71$
Ответ: относительная частота $W_5 = 0,71$ .

6. Вычисление относительной частоты для $N = 1000$

Дано:
- $M = 698$ — количество успешных событий (падений призмы на боковую грань),
- $N = 1000$ — количество испытаний.

Шаги вычисления:

Подставляем данные в формулу:
$W_6 = \frac{M}{N} = \frac{698}{1000}$
Выполняем деление:
$W_6 = 0,698$
Округляем результат до сотых:
$W_6 \approx 0,70$
Ответ: относительная частота $W_6 = 0,70$ .

Итоговая таблица:

Число испытаний $N$	10	50	100	300	500	1000
Частота падения призмы на любую боковую грань $M$	8	34	73	206	353	698
Относительная частота падения призмы на боковую грань $W$	0,80	0,68	0,73	0,69	0,71	0,70

По приведенной таблице видно, что относительная частота падения призмы на боковую грань при увеличении числа испытаний $N$ стабилизируется и стремится к числу 0,7. Это означает, что с увеличением числа испытаний частота события $A$ (падение призмы на боковую грань) приближается к вероятности события $P(A)$ .

Ответ: $P(A) = 0,7$ .

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Задачи для внеклассной работы