ГДЗ по Алгебре 10-11 Класс Учебник 📕 Алимов — Все Части

Алгебра

10-11 класс учебник Алимов

10 класс

Тип

ГДЗ, Решебник.

Автор

Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.

Год

2015-2024.

Издательство

Просвещение.

Описание

Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.

Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.

Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.

Преимущества учебника

Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения.
Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач.
Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам.
Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры.
Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.

Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.

ГДЗ по Алгебре 10-11 Класс Номер 1157 Алимов — Подробные Ответы

Задача

Заполнить последний столбец таблицы (с точностью до тысячных):

Краткий ответ:

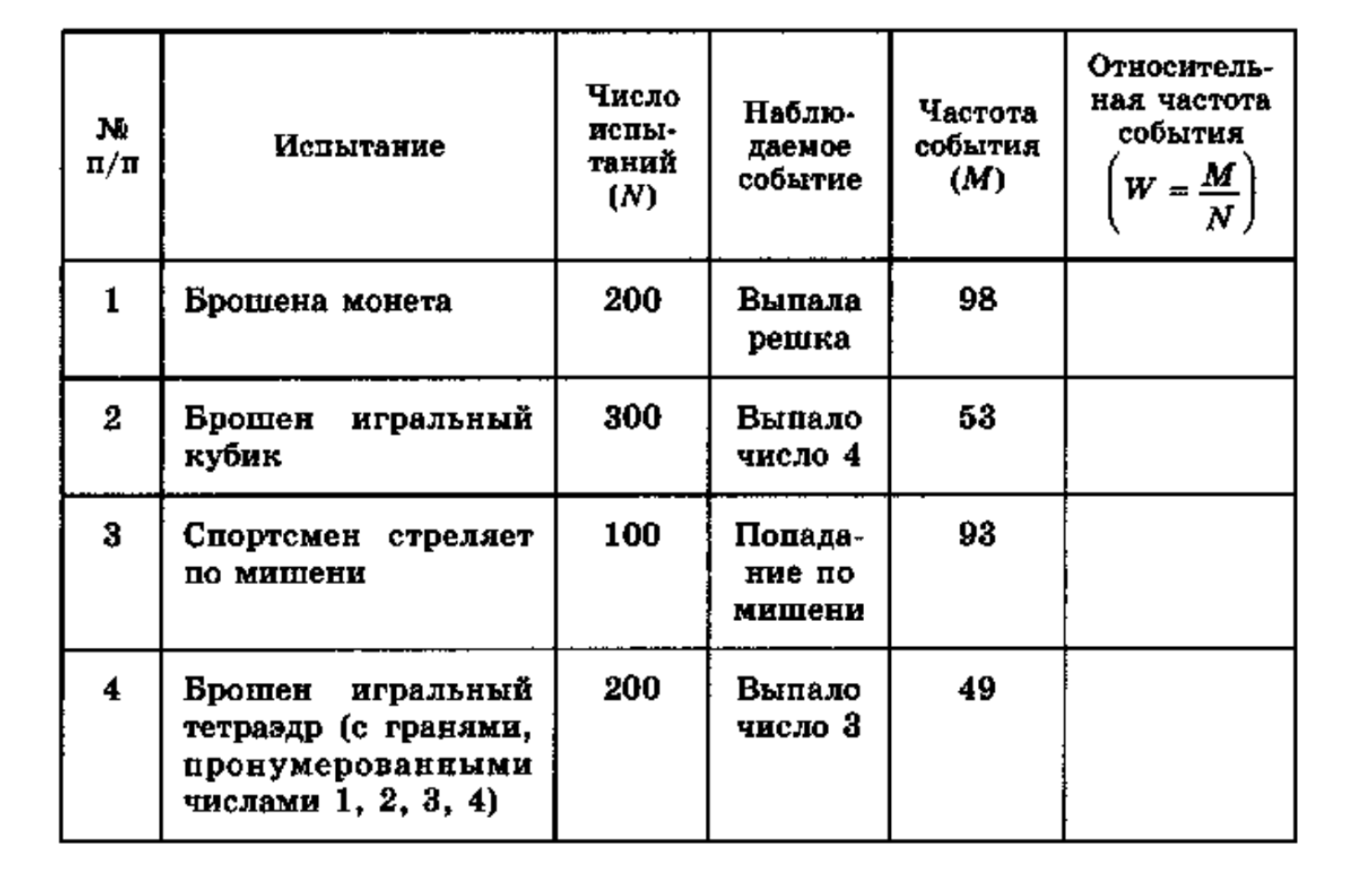
№ п/п	Испытание	Число испытаний (N)	Наблюдаемое событие	Частота события (M)	Относительная частота события $W_{} = \frac{M}{N}$
1	Брошена монета	200	Выпала решка	98	0,490
2	Брошен игральный кубик	300	Выпало число 4	53	0,176
3	Спортсмен стреляет по мишени	100	Попадание по мишени	93	0,930
4	Брошен игральный тетраэдр	200	Выпало число 3	49	0,245

$W_{1} = \frac{M}{N} = \frac{98}{200} = \frac{49}{100} = 0, 49;$

$W_1 = \frac{M}{N} = \frac{98}{200} = \frac{49}{100} = 0,49;$ $W_{2} = \frac{M}{N} = \frac{53}{300} = 0, 17 (6) \approx 0, 176;$

$W_2 = \frac{M}{N} = \frac{53}{300} = 0,17(6) \approx 0,176;$ $W_{3} = \frac{M}{N} = \frac{93}{100} = 0, 93;$

$W_3 = \frac{M}{N} = \frac{93}{100} = 0,93;$ $W_4 = \frac{M}{N} = \frac{49}{200} = 0,245;$

Подробный ответ:

Необходимо заполнить последний столбец таблицы, который содержит значения относительных частот события для каждого испытания. Мы будем использовать формулу для вычисления относительной частоты:

$W = \frac{M}{N}$

где:

$M$ — количество успешных событий (наблюдаемое количество событий),
$N$ — общее количество испытаний (всего выполнено испытаний).

В таблице даются различные виды испытаний с числом испытаний $N$ и количеством успешных событий $M$ . Мы должны вычислить относительные частоты для каждого испытания с точностью до тысячных.

1. Первая строка (Испытание: Брошена монета)

№ п/п	Испытание	Число испытаний $N$	Наблюдаемое событие	Частота события $M$	Относительная частота события $W$
1	Брошена монета	200	Выпала решка	98	0,490

Дано:

Общее количество испытаний $N = 200$ ,
Количество успешных событий $M = 98$ .

Шаги:

Используем формулу для вычисления относительной частоты:
$W_1 = \frac{M}{N} = \frac{98}{200}$
Выполним деление:
$\frac{98}{200} = 0,49$
Ответ: относительная частота события — $W_1 = 0,490$ (с точностью до тысячных).

2. Вторая строка (Испытание: Брошен игральный кубик)

№ п/п	Испытание	Число испытаний $N$	Наблюдаемое событие	Частота события $M$	Относительная частота события $W$
2	Брошен игральный кубик	300	Выпало число 4	53	0,176

Дано:

Общее количество испытаний $N = 300$ ,
Количество успешных событий $M = 53$ .

Шаги:

Используем формулу для вычисления относительной частоты:
$W_2 = \frac{M}{N} = \frac{53}{300}$
Выполним деление:
$\frac{53}{300} = 0,176666\ldots$
Округлим результат до тысячных:
$0,176666\ldots \approx 0,176$
Ответ: относительная частота события — $W_2 = 0,176$ .

3. Третья строка (Испытание: Спортсмен стреляет по мишени)

№ п/п	Испытание	Число испытаний $N$	Наблюдаемое событие	Частота события $M$	Относительная частота события $W$
3	Спортсмен стреляет по мишени	100	Попадание по мишени	93	0,930

Дано:

Общее количество испытаний $N = 100$ ,
Количество успешных событий $M = 93$ .

Шаги:

Используем формулу для вычисления относительной частоты:
$W_3 = \frac{M}{N} = \frac{93}{100}$
Выполним деление:
$\frac{93}{100} = 0,93$
Ответ: относительная частота события — $W_3 = 0,930$ .

4. Четвертая строка (Испытание: Брошен игральный тетраэдр)

№ п/п	Испытание	Число испытаний $N$	Наблюдаемое событие	Частота события $M$	Относительная частота события $W$
4	Брошен игральный тетраэдр	200	Выпало число 3	49	0,245

Дано:

Общее количество испытаний $N = 200$ ,
Количество успешных событий $M = 49$ .

Шаги:

Используем формулу для вычисления относительной частоты:
$W_4 = \frac{M}{N} = \frac{49}{200}$
Выполним деление:
$\frac{49}{200} = 0,245$
Ответ: относительная частота события — $W_4 = 0,245$ .

Итоговая таблица:

№ п/п	Испытание	Число испытаний $N$	Наблюдаемое событие	Частота события $M$	Относительная частота события $W$
1	Брошена монета	200	Выпала решка	98	0,490
2	Брошен игральный кубик	300	Выпало число 4	53	0,176
3	Спортсмен стреляет по мишени	100	Попадание по мишени	93	0,930
4	Брошен игральный тетраэдр	200	Выпало число 3	49	0,245

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Задачи для внеклассной работы